Varianta 152

Prof.  Ştefan Maria Lăcrămioara

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(4,8\cdot 2,5-7\) este…

(5p)     2. Numărul iraţional din mulţimea \(M=\left\{ -5;-\frac{\sqrt{81}}{12};\sqrt{16-{{2}^{4}}};\sqrt{243};25 \right\}\) este….

(5p)     3. Media aritmetică a numerelor \(a=5+3\sqrt{2}\) şi \(b=5-3\sqrt{2}\) este……

(5p)     4. Lungimea liniei mijlocii în trapezul ABCD este de 7 cm, atunci suma lungimilor bazelor  este de …..cm

(5p)     5. În paralelipipedul dreptunghic ALGEBRIC  din Figura 1 se cunosc AL = LG = \(6\sqrt{2}\) cm, IG = \(12\sqrt{3}\) cm, atunci măsura unghiului IAG = …..⁰.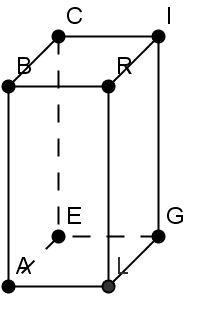                                                                                        

Figura 1

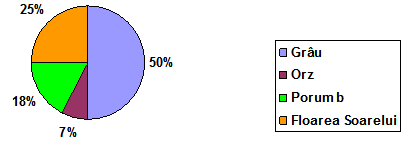
(5p)     6.  În diagrama alăturată este reprezentată repartizarea unui teren agricol de 240 ha în funcţie de culturi. Suprafaţa cultivată cu floarea soarelui este de ….ha.

         SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi un tetraedru regulat GEOM.

(5p)     2. Rezolvaţi în mulţimea numerelor reale inecuaţia \(\left| \frac{2x+3}{5} \right|\le 3\).

(5p)     3. Un caiet costă 1,8 lei, iar un pix de 3 ori mai mult. Calculaţi cât ar costa 5 caiete şi 4 pixuri împreună.

 4. Se dă funcţia \(f:\mathbb{R}\to \mathbb{R}\), \(f\left( x \right)=2x-5\). Calculaţi:

(5p)    a) Coordonatele punctului A în care graficul funcţiei intersectează axa ordonatelor şi coordonatele punctului B în care graficul funcţiei intersectează axa absciselor.

(5p)    b) Aria triunghiului determinat de graficul funcţiei şi axele de coordonate.

(5p)     5.  Arătaţi că numărul \(n=\sqrt{{{\left( 3\sqrt{3}-5 \right)}^{2}}}+3\cdot \sqrt{{{\left( \sqrt{3}-2 \right)}^{2}}}\) este pătrat perfect.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. În Figura 2 este reprezentat un teren în formă de trapez dreptunghic ABCD, cu BC = 24 m , \(m\left( \measuredangle A \right)={{60}^{o}}\), AC este bisectoarea unghiului BAD

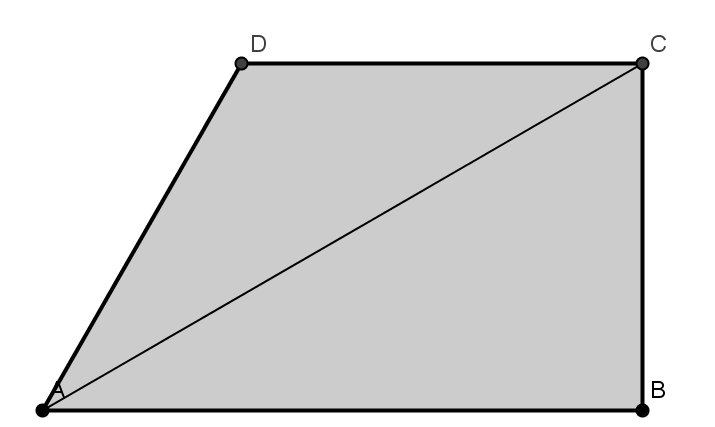
 Figura 2

 (5p)  a) Calculaţi lungimea gardului pe linia diagonalei AC.

 (5p)  b) Arătaţi că AD = DC = \(16\sqrt{3}\)

 (5p)  c) Verificaţi dacă 120 m plasă de sârmă este suficient pentru împrejmuirea exterioară a terenului.

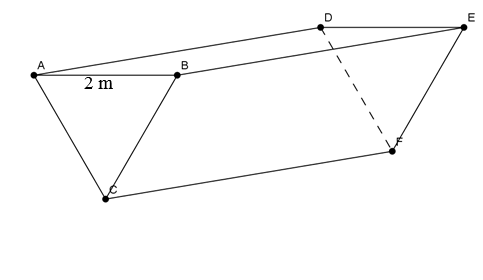
 2. În Figura 3 este reprezentat un canal de alimentare cu apă al unei instalaţii hidraulice cu secţiunea triunghi echilateral de latură AB = 2m  şi având lungimea de 1 km. \(\left( \sqrt{3}\approx 1,73 \right)\)

Figura 3

(5p)  a) Aflaţi aria cimentată a pereţilor canalului pe o lungime de 1 km.

5p)  b) Aflaţi volumul canalului.

(5p)  c) Aflaţi debitul canalului în m³/h, dacă apa curge cu 2 m/s.