Varianta 153

Prof.  Ştefan Maria Lăcrămioara

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\left( 2x+3y \right)-3\left( x+y \right)\) este ……………

(5p)     2. Valoare numărului  natural x pentru care \(\overline{219x}\) este divizibil cu 18 este ……

(5p)     3. Dintre numerele reale \(x=4\sqrt{5}\) şi \(y=9\) mai mic este……….

(5p)     4. Perimetrul triunghiului echilateral cu latura de \(3\sqrt{5}cm\) este …….cm.

(5p)     5. Diagonala cubului ABCDA’B’C’D’ cu muchia AB = \(2\sqrt{3}cm\) este de …..cm.

(5p)     6. În tabelul de mai jos sunt cuprinse numărul de piese realizate de muncitorii dintr-un atelier în decursul acestei  săptămâni:

În această săptămână muncitorii au realizat în medie un număr de …. piese.

           SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o piramidă triunghiulară regulată cu baza ABC şi vârf S.

(5p)     2. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R}\), \(f\left( x \right)=\frac{2}{3}x-7\). Calculaţi \(f\left( 0 \right)-2\cdot f\left( 3 \right)\).

(5p)     3. Să se determine două numere ştiind că primul este cu 11,6 mai mare decât al doilea şi media aritmetică a celor două numere este 31,7.

 4. Se consideră expresia \(E\left( x \right)=\left( \frac{1}{x+1}-\frac{4}{1-x} \right):\frac{3x-1}{{{x}^{2}}-1}\), \(x\in \mathbb{R}\backslash \left\{ -1;\frac{1}{3};1 \right\}\).

(5p)    a) Arătaţi că forma cea mai simplă a expresie este \(E\left( x \right)=\frac{5x+3}{3x-1}\)

(5p)    b) Determinaţi numerele naturale x pentru care \(E\left( x \right)\in \mathbb{N}\).

(5p)     5. Arătaţi că numărul \(n=\sqrt{1+3+5+7+...+4021}\) este număr natural.

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

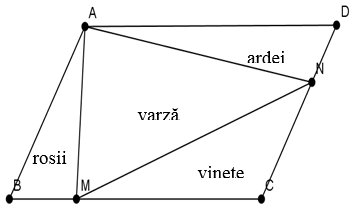
1. O grădină are forma unui paralelogram (Figura 1), cu latura AB = 9 m şi latura AD = 15. Acest teren se împarte astfel: Pe latura BC se ia punctul M la o distanţă de 5 m faţă de punctul B, iar pe latura CD se ia punctul N la 6 m faţă de punctul C.

Pe loturile astfel obţinute se cultivă zarzavaturi.

Figura 1

 (5p)  a) Calculaţi aria triunghiului MNC în funcţie de aria paralelogramului.

 (5p)  b) Arătaţi că suprafaţa cultivată cu roşii este egală cu suprafaţa cultivată cu ardei.

 (5p)  c) Arătaţi că suprafaţa cultivată cu vinete este jumătate din suprafaţa cultivată cu varză.

 2. În Figura 2 este reprezentat un siloz de cereale în formă de prismă patrulateră regulată, cu dimensiunile AB = 4 m, AE = 5m, în care se depozitează grâu, având masa hectolitrică 72 kg/hl (masa hectolitrică sau masa volumetrică reprezintă masa unui hectolitru de cereale). 

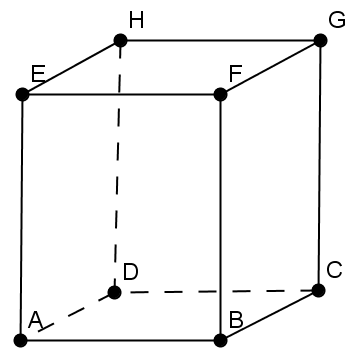
Figura 2

(5p)  a) Aflaţi volumul silozului.

(5p)  b) Aflaţi câte tone de grâu există în siloz, dacă acesta se încarcă 90% din capacitate.

(5p)  c) Dacă din depozit se livrează zilnic câte 12,8 t de grâu pentru panificaţie, calculaţi după câte zile grâul rămas va reprezenta \(\frac{1}{3}\) din cantitatea iniţială