Varianta 155

Prof.  Ştefan Maria Lăcrămioara

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Cel mai mic număr întreg de două cifre este …..

(5p)     2. Soluţia pozitivă a ecuaţiei \(5-{{x}^{2}}=-4\) este…..

(5p)     3. Partea fracţionară a numărului \(a=3,37\) este…..

(5p)     4. Fie \(ABCD\) un romb cu \(AB=6\)cm şi \(m\left( {\hat{A}} \right)=60{}^\circ \), atunci \(P\left( \Delta ABD \right)\) este …..cm.

(5p)     5. Se consideră prisma triunghiulară \(ABCA'B'C'\) (Figura 1). Fie \(M\) mijlocul lui \(\left[ B'C' \right]\) şi \(N\) mijlocul lui \(BC\). Dacă \(AA'=6\) şi \(AB=4\sqrt{3}\) atunci \(m\left( \measuredangle AM;\left( ABC \right) \right)\) este  …..\({}^\circ \)

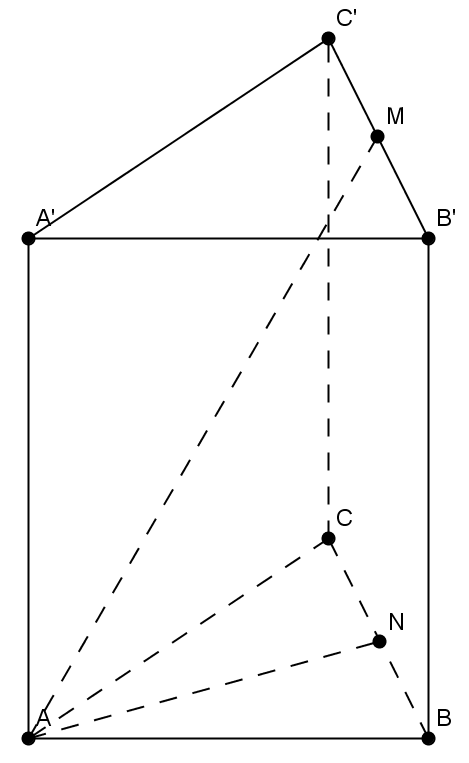
Figura 1

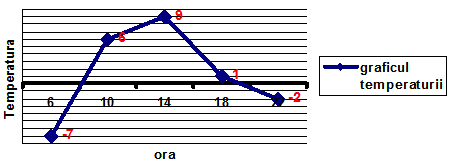
(5p)     6. În graficul de mai jos este reprezentată temperatura înregistrată pe parcursul unei zile. Diferenţa dintre temperatura maximă şi minimă este de ….. \({}^\circ \)C.

           SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen o primă patrulateră regulată \(ABCDA'B'C'D'\).

(5p)     2. Se consideră mulţimile \(A=\left\{ \left. x\in \mathbb{Z} \right|\left| 2x-7 \right|\le 5 \right\}\) şi \(B=\left\{ \left. y\in \mathbb{Z} \right|y=x-3;x\in A \right\}\). Enumeraţi elementele mulţimii \(A\cap B\).

(5p)  3.Determinaţi cel mai mic număr care împărţit la 7 dă restul 3 şi împărţit la 9 dă restul 5.

 4. Fie funcţia \(f:\mathbb{R}\to \mathbb{R};\)\(f\left( x \right)=3-2x\).

(5p)    a) Reprezentaţi grafic funcţia într-un sistem de axe ortogonale.

(5p)    b) Determinaţi distanţa de la originea sistemului la \({{G}_{f}}\).

(5p)     5. Determinaţi numărul natural \(n\) astfel încât \(\frac{\sqrt{2}-\sqrt{1}}{\sqrt{2}}+\frac{\sqrt{3}-\sqrt{2}}{\sqrt{6}}+...+\frac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n\left( n+1 \right)}}=\frac{9}{10}\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. În Figura 2 este reprezentată schiţa unei terase în formă de triunghi dreptunghic \(\Delta ABC\) cu \(m\left( {\hat{B}} \right)=90{}^\circ \), având \(AB=6\)m, \(BC=24\)m. Se ridică un perete \(MN\) pe linia paralelă cu \(AB\).

(5p)  a) Calculaţi suprafaţa terasei.

 (5p)  b) Determinaţi distanţa \(BN\) astfel încât cele două suprafeţe obţinute să fie egale.

 (5p)  c) Suprafaţa \(AMNB\) se acoperă cu mochetă. Aflaţi costul ştiind că preţul mochetei este de 18,75 lei/m².

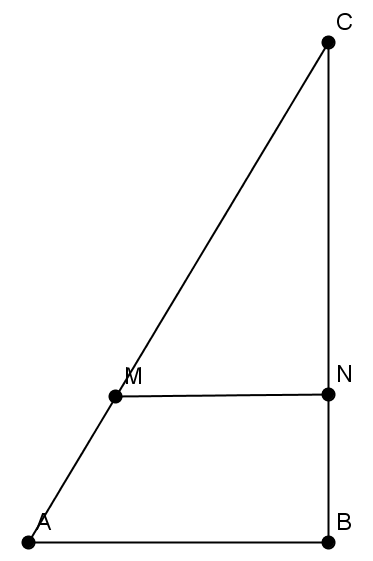
Figura 2  

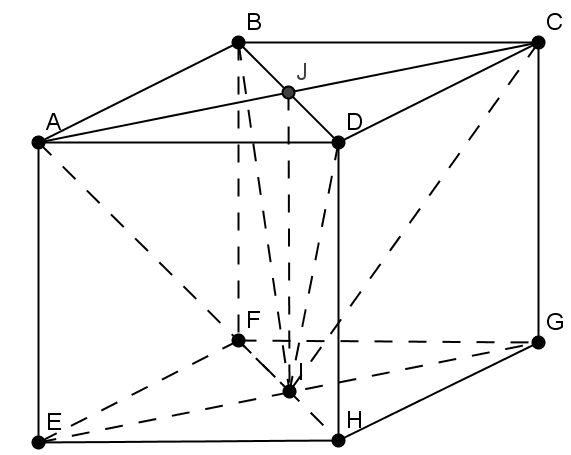
2. În Figura 3 este reprezentată o cutie sub formă de cub în care există o cavitate pentru o piatră preţioasă în formă de piramidă patrulateră regulată. Muchia cubului este de \(AB=6\) cm.

(5p)  a) Calculaţi volumul pietrei preţioase.

 (5p)  b) Se poleieşte cutia cu un material aurifer. Ştiind că materialul costă 250 lei/m², calculaţi preţul.

 (5p)  c) Cutia se umple cu un material granulos astfel încât să rămână spaţiul liber pentru piatra preţioasă. Calculaţi volumul materialului granulos.