Varianta 157

Prof: Telteu Constantin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1.    \(\frac{1}{4}:\frac{1}{2}-\frac{1}{2}=...\)

(5p)     2.  \(Card\,\left( \mathbb{Z}\cap \left[ -10;10 \right] \right)=...\)

(5p)     3.   5 kg de mere costă cât 10 kg de prune, iar un kg de prune costă 1,5 lei. Câţi lei costă un kg de mere?

(5p)     4.  Un dreptunghi are lăţimea cu 80% mai mică decât lungimea, care este de 100 cm. Aria sa este de … \(c{{m}^{2}}\).

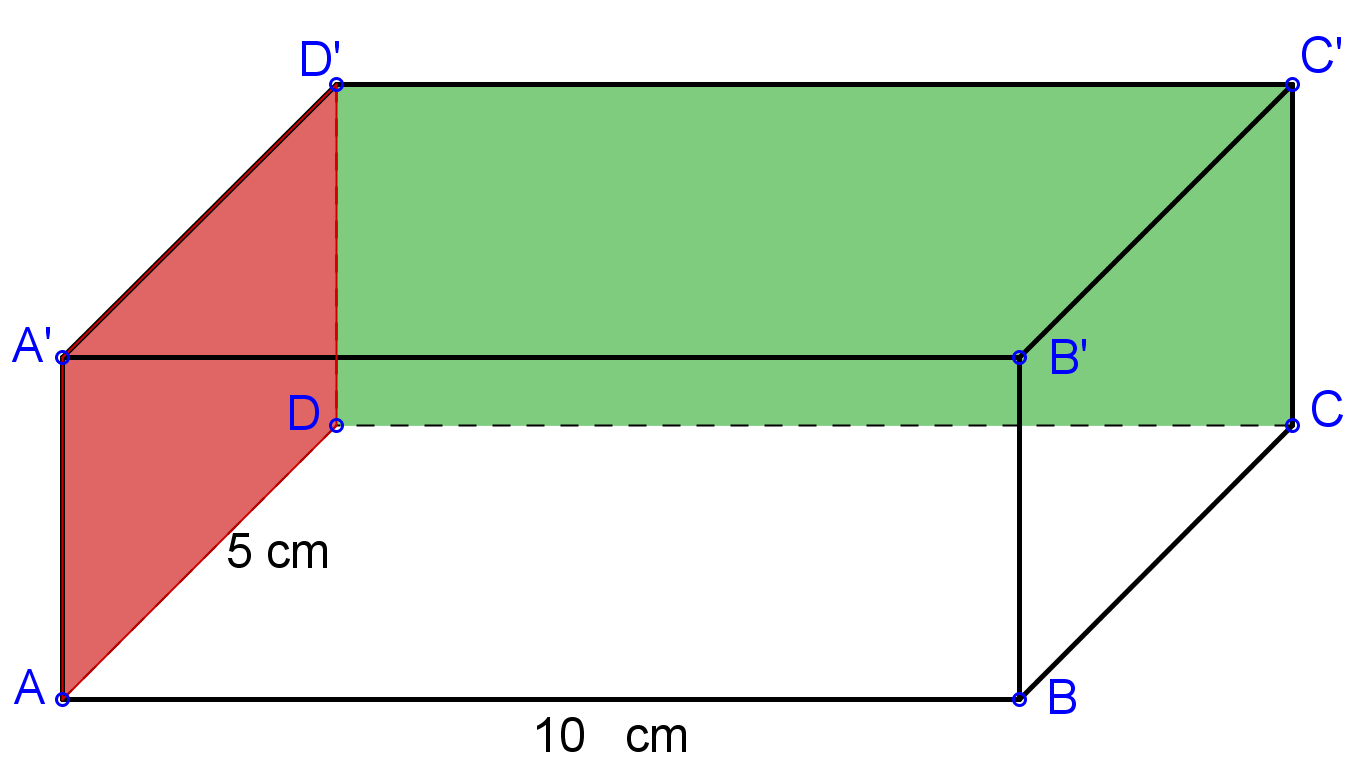
(5p)     5. În figura următoare perimetrul feţei roşii este de 30 cm. Aria feţei verzi este de … \(c{{m}^{2}}\) .

(5p)     6. În tabelul următor, sunt trecute notele obţinute la un test de către elevii unei clase.

Media clasei este…

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen un dreptunghi ABCD şi o perpendiculară pe planul său ce conţine punctul de intersecţie al diagonalelor.

(5p)     2. Calculaţi media geometrică a numerelor \(x=3-\sqrt{8}\) şi \(y=3+2\sqrt{2}\).

(5p)     3.  Deschid o carte de 100 pagini la întâmplare de cinci ori. De fiecare dată îmi notez numerele cu care sunt numerotate paginile. Adun apoi toate aceste numere. Se poate să obţin ca rezultat numărul 945? Dar numărul 100? Argumentaţi.

 4. Se dau funcţiile: \(f,g:\mathbb{R}\to \mathbb{R},\,f\left( x \right)=x+1,\,\,g\left( x \right)=-x-2\).

(5p)    a)   Reprezentaţi graficele funcţiilor pe acelaşi sistem de axe de coordonate.

(5p)    b)  Aflaţi distanţa de la punctul de intersecţie al graficelor celor două funcţii la axa Oy.

(5p)     5. Media aritmetică a două numere pozitive este dublul unuia dintre ele. Ştiind că cel mic este \({{\left( \sqrt{2} \right)}^{-4}}\), aflaţi celălalt număr.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. O piesă metalică are forma ( vezi figura) unei prisme triunghiulare regulate \(ABCA'B'C'\) din care s-a scos piramida triunghiulară regulată \(OA'B'C'\) (O centrul bazei ABC). Toate muchiile prismei sunt de 6 cm.

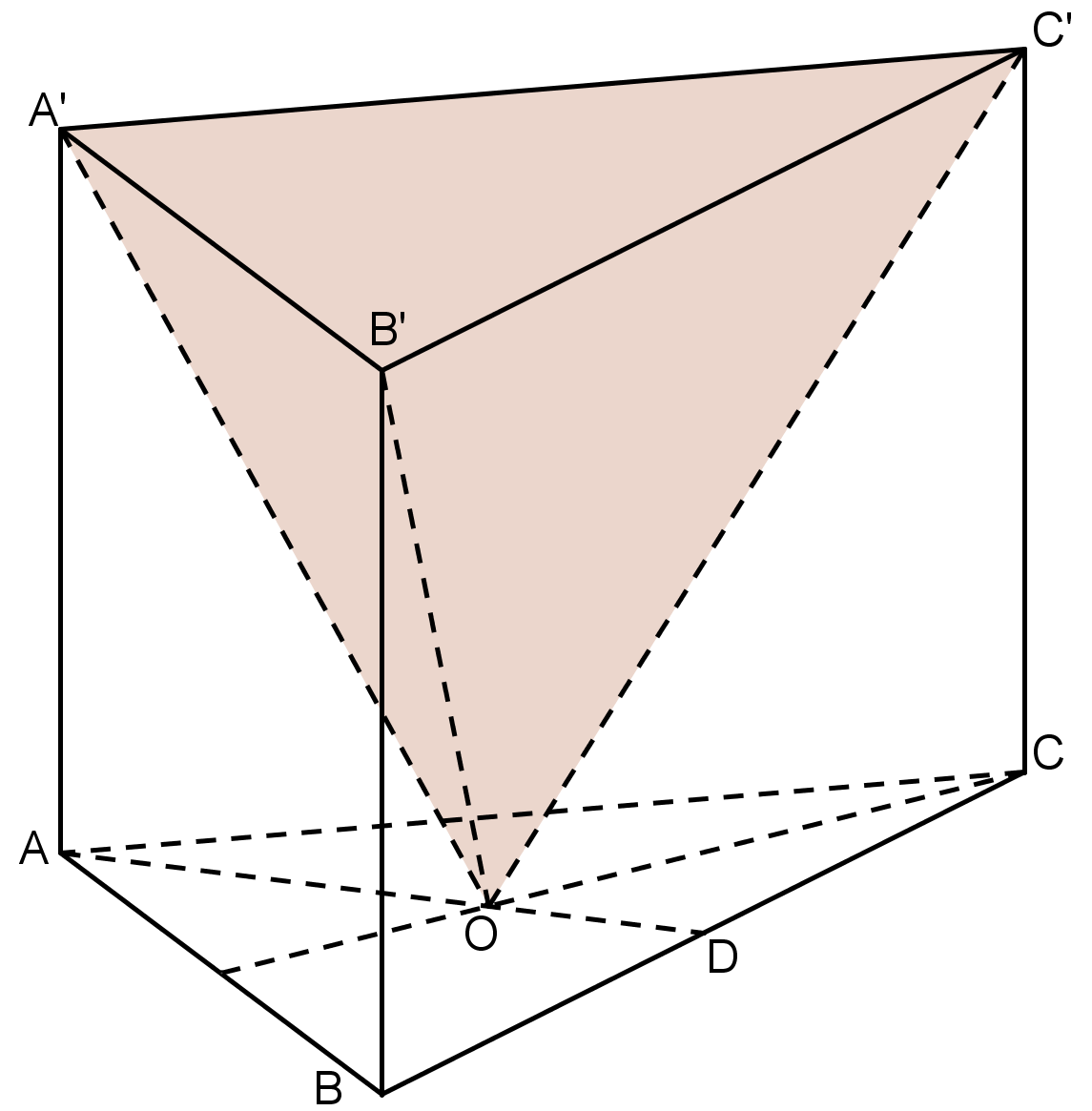
(5p)  a) Calculaţi volumul piesei.

 (5p)  b) Vopsim piesa în întregime. Ce suprafaţă avem de vopsit?

 (5p)  c)  Care este distanţa de la vârful C la faţa \(\left( OB'C' \right)\)?

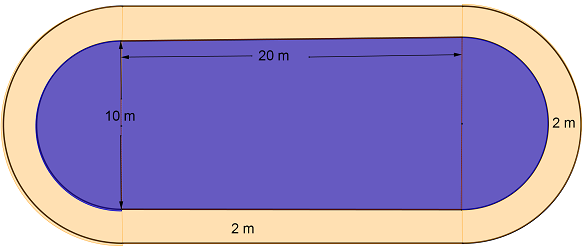
 2. Conturul  bazinului de înot din figură are forma unui dreptunghi completat la capete cu câte un semicerc. Împrejurul bazinului este o bandă de nisip cu lăţimea constantă de 2 m. Dreptunghiul are lungimea de 20 m şi lăţimea de 10 m.

(5p)  a) Ce suprafaţă are bazinul?

(5p)  b) Care este suprafaţa acoperită cu nisip?

(5p)  c) Care este diferenţa dintre perimetrul exterior al benzii de nisip şi cel interior?