Varianta 158

Prof: Telteu Constantin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. \(-\frac{1}{2}-\frac{1}{2}+\frac{1}{2}\cdot \frac{1}{2}=\)…

(5p)     2.  Dintre fracţiile \(\frac{178}{829}\) şi \(\frac{7}{6}\), mai mică este…

(5p)     3. Dacă un creion şi un stilou costă 10 lei, iar două creioane şi un stilou costă 11 lei, câţi lei costă un stilou?

(5p)     4. Un pătrat cu aria de \(3\,\,c{{m}^{2}}\)are perimetrul de … cm

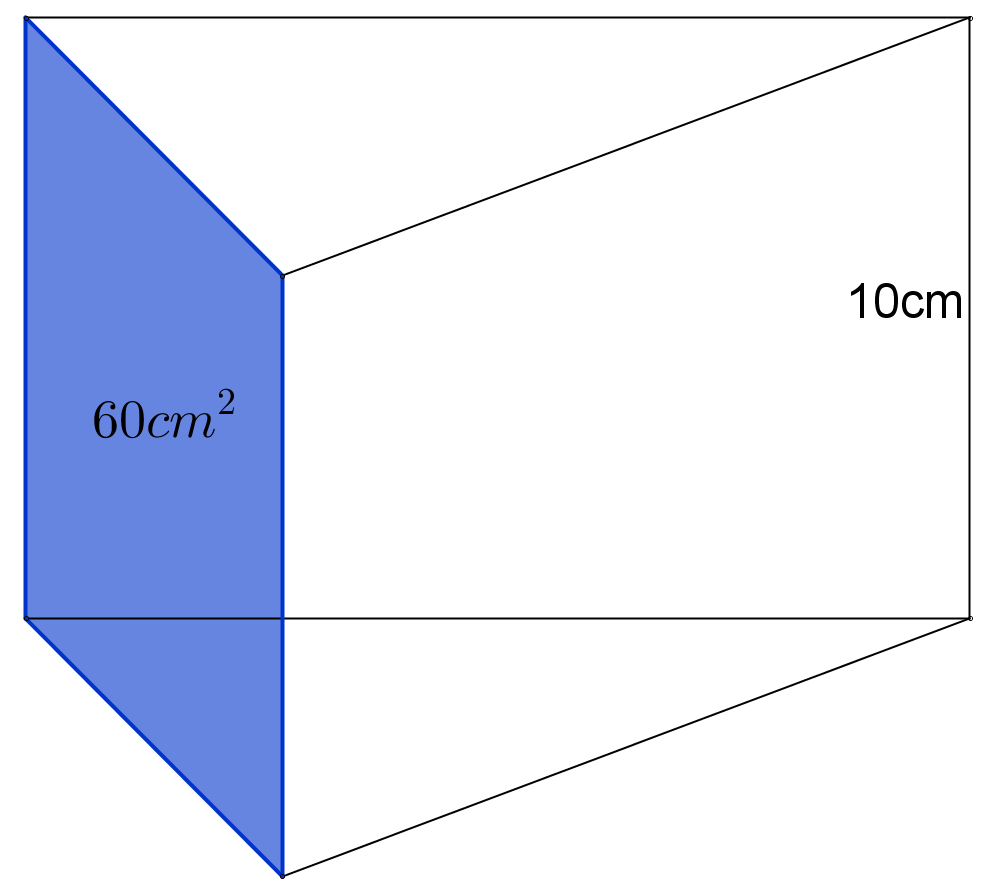
(5p)     5. Prisma triunghiulară regulată din figură  are aria feţei albastre  de \(60\,\,c{{m}^{2}}\). Cât este aria bazei ei?

(5p)     6. Diagrama următoare arată numărul de elevi înscrişi la fiecare disciplină la un liceu sportiv (fiecare elev este înscris la o singură disciplină).

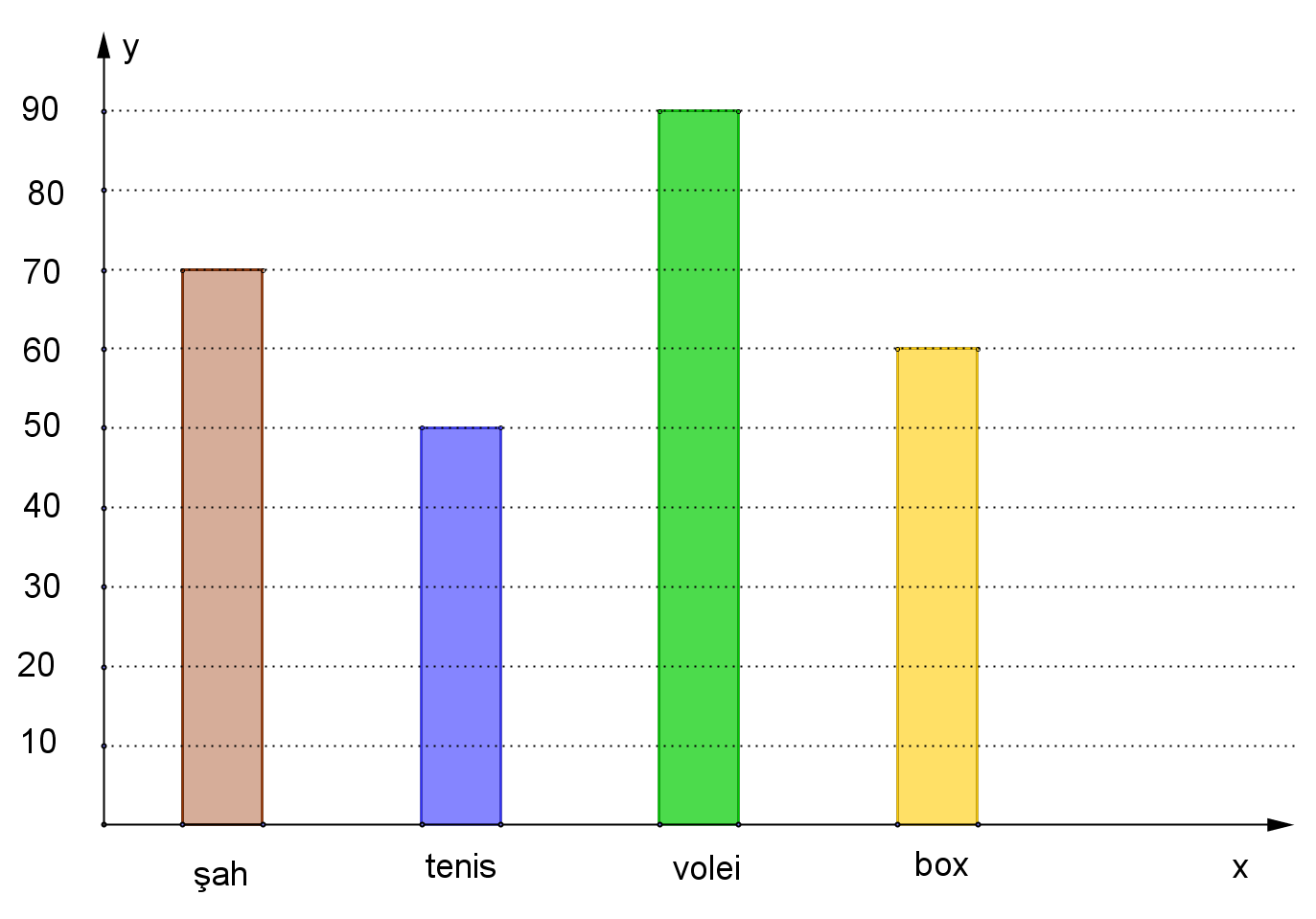
Câţi elevi sunt în acest liceu?

        SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1.  Desenaţi un triunghi dreptunghic şi o perpendiculară pe planul său ce trece prin vârful unghiului drept.

(5p)     2.  Scrieţi în ordine crescătoare numerele: \(x=2-\frac{1}{2}-\frac{1}{\frac{1}{2}};\,\,\,y=3-\frac{1}{3}-\frac{1}{\frac{1}{3}};\,\,z=\sqrt{2}-\frac{1}{\sqrt{2}}-\frac{1}{\frac{1}{\sqrt{2}}}.\)

(5p)     3. Într-un grup de 9 fete şi 13 băieţi, care într-o excursie au făcut 373 poze în total, fetele au făcut acelaşi număr de poze fiecare, iar fiecare băiat a făcut cu 5 poze mai multe ca o fată. Câte poze a făcut o fată?

4. Fie funcţia: \(f:\mathbb{R}\to \mathbb{R},\,f\left( x \right)=ax+3;\,a\in \mathbb{R}.\)

(5p)    a) Să se determine , astfel încât \({{G}_{f}}\bigcap Ox=\left( -1;0 \right)\).

(5p)    b) Să se determine , astfel încât punctul \(A\left( 2;\,\,5-a \right)\in {{G}_{f}}\).

(5p)     5. Dacă \(x=a+\frac{1}{a}\) şi \(y=a-\frac{1}{a}\), calculaţi \({{x}^{2}}+{{y}^{2}}\) pentru \(a=\sqrt{2}\).

     SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Dintr-un bloc de piatră în formă de paralelipiped dreptunghic \(ABCDA'B'C'D'\)(vezi figura) cu \(L=10\,dm,\,\,\,l=h=5\,\,dm\) s-a cioplit porţiunea în formă de paralelipiped dreptunghic \(EFGHE'F'G'H'\), cu dimensiunile de pe figură.

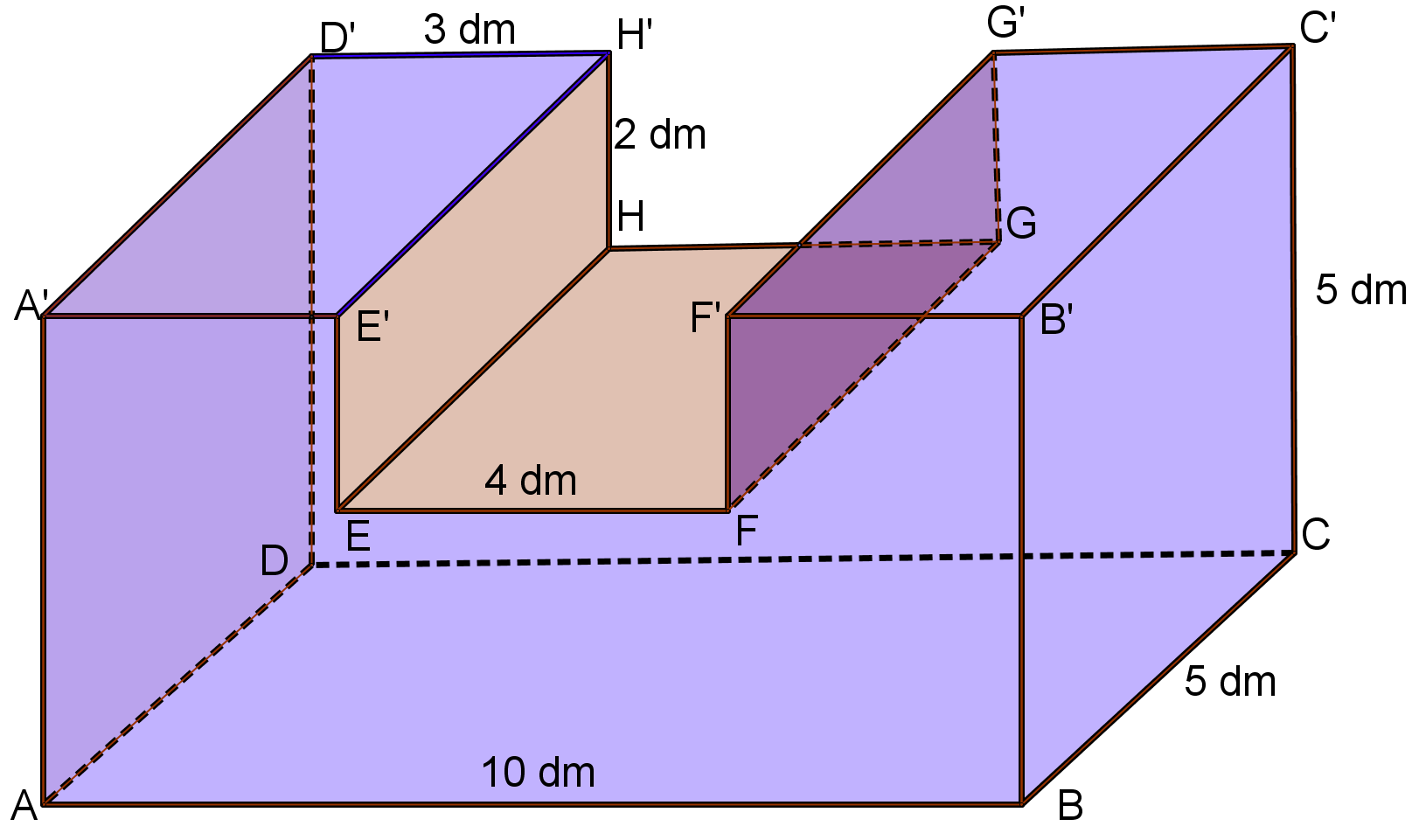
 (5p)  a) Aflaţi volumul corpului rămas.

 (5p)  b) Aflaţi suprafaţa totală a corpului.

 (5p)  c) Calculaţi distanţa FC.

 2. Curtea unui hotel are forma de trapez dreptunghic (vezi figura), cu diagonalele perpendiculare. Trapezul are baza mică de 10 cm şi înălţimea de 20 cm.

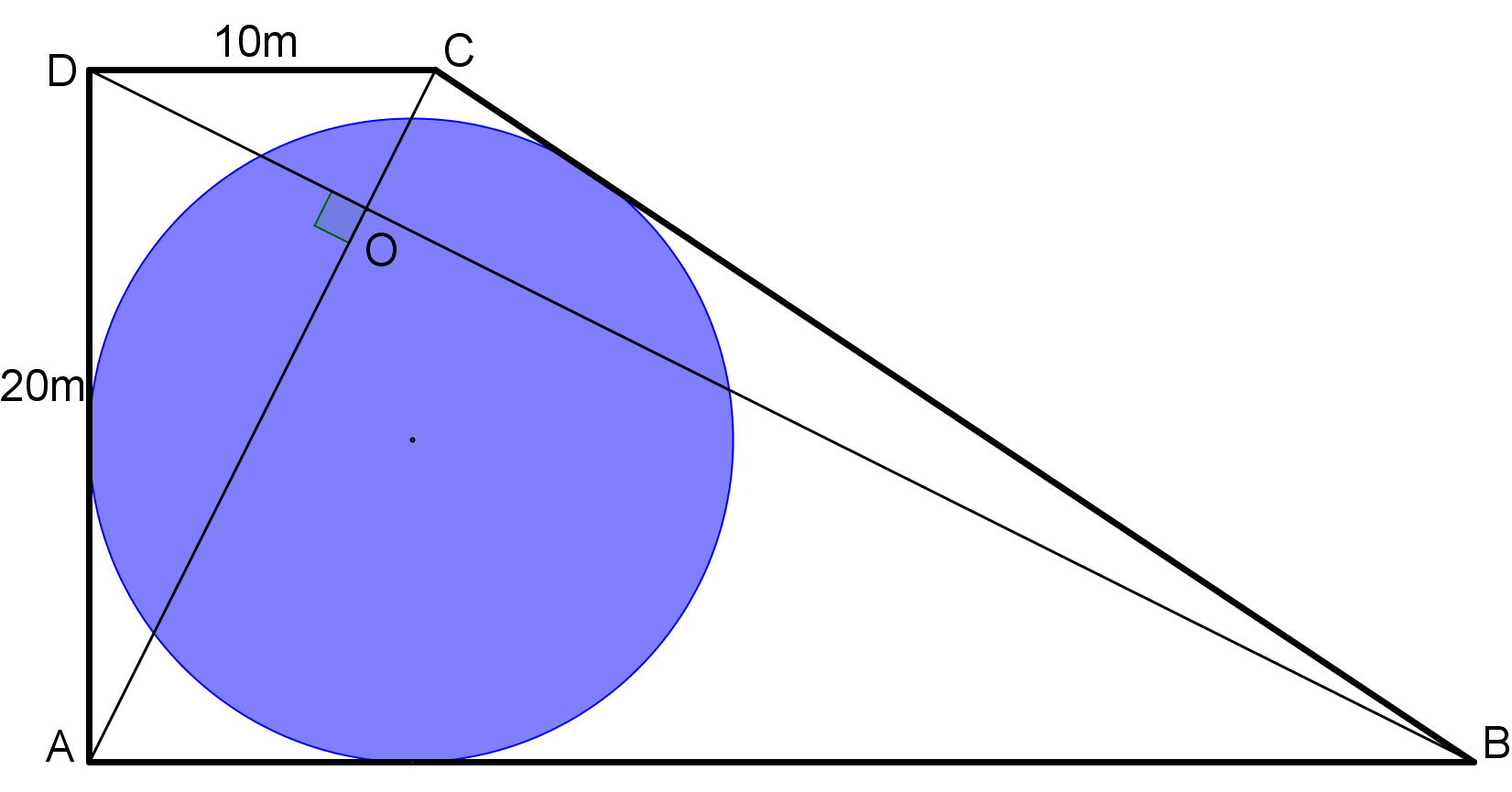
(5p)  a) Calculaţi diagonalele acestui trapez.

(5p)  b) Ce lungime ar avea un gard care ar împrejmui această curte?

(5p)  c) Proprietarul hotelului vrea să amenajeze în curte o piscină circulară cât mai mare posibilă. Care va fi raza ei?