Varianta 161

Prof:C. Telteu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Să se determine soluţia ecuaţiei: \(5-x+11-13=22-33\)

(5p)     2. Andrei şi Irina numără stelele de pe cer. La un moment dat, Andrei numărase 150 de stele, iar Irina cu 25 mai puţine. Câte stele număraseră ei împreună?

(5p)     3. Un număr par este şi multiplu de 11, iar următorul număr par, este multiplu de 5. Un exemplu este  numărul 418? Găsiţi cel mai mic număr cu aceste proprietăţi.

(5p)     4. Diagonala unui pătrat este de \(10\sqrt{2}\) cm. Perimetrul său este de…

(5p)     5. Un vas în formă de paralelipiped dreptunghic are \(L=2l=1\,m\), iar \(h=2\,m\). Încerc să pun în el 1000 litri de apă. Încap?

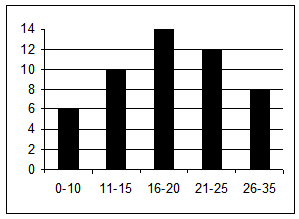
(5p)     6. Priviţi diagrama următoare, în care este redată frecvenţa intrărilor pe messenger a prietenilor lui Andrei şi numărul lor într-o lună. (orizontală - nr. intrări, verticală – nr. prieteni) Spunem că un prieten al lui Andrei este „mai aparte” dacă are cel mult 10 intrări, sau mai mult de 25.

Câţi astfel de prieteni „mai aparte” are Andrei?

  SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o piramidă patrulateră regulată \(VABCD\) şi o apotemă a sa \(VM\).

(5p)     2. Dacă \(M\) este mulţimea soluţiilor ecuaţiei \(x-3=4\) iar \(B=\left\{ 1,2,3,4 \right\}\), atunci \(B\backslash M=....\)

(5p)     3. 10% din elevii unei şcoli de artă sunt pasionaţi doar de pictură, 15% sunt pasionaţi doar de muzică şi 100 elevi doar de balet. Restul, care reprezintă  jumătate din elevii şcolii, au mai multe pasiuni . Câţi elevi sunt în acea şcoală?          

4. Se dă funcţia \(f:\mathbb{R}\to \mathbb{R};\,\,f\left( x \right)=x-\sqrt{2},\forall x\in \mathbb{R}\).

(5p)    a) Determinaţi pe \(a\in \mathbb{R}\) astfel încât \(M\left( \sqrt{2};a \right)\in {{G}_{f}}\).

(5p)    b)  Determinaţi \(b\in \mathbb{R}\) astfel încât \(M\left( b,f\left( b \right) \right)\) să fie situat sub axa \(Ox\).

(5p)     5. Verificaţi identitatea: \({{\left( \frac{x-1}{x+1} \right)}^{2}}-2+{{\left( \frac{x+1}{x-1} \right)}^{2}}-{{\left( \frac{4x}{{{x}^{2}}-1} \right)}^{2}}=0\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. O portocală perfect sferică se taie în două părţi identice. Uneia dintre acestea i se scoate miezul, obţinându-se astfel un „pahar” . Coaja portocalei are peste tot grosimea de 5 mm, iar diametrul portocalei era de 9 cm.

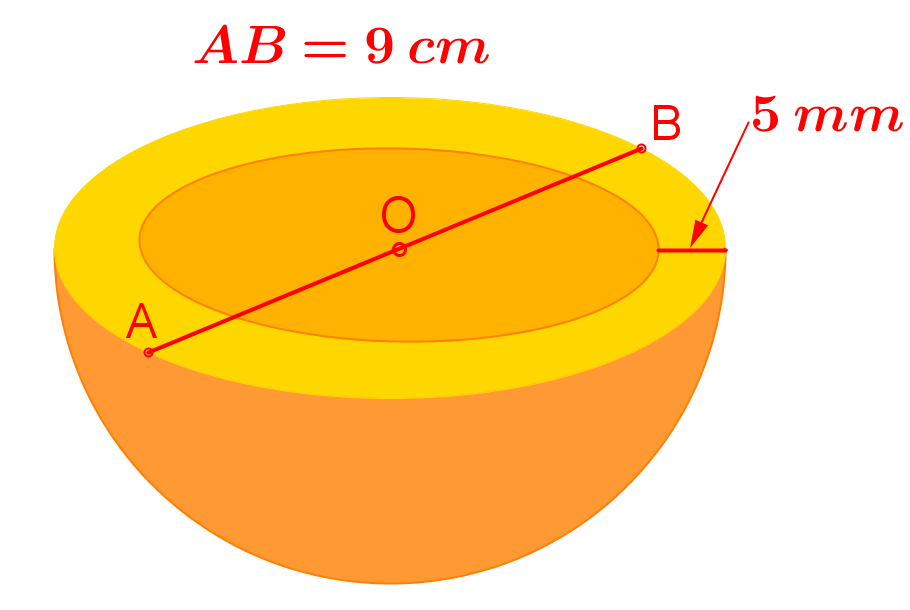
1. a) Ce volum avea coaja portocalei pe care am tăiat-o? (\(\pi \approx 3,14\))

1. b) Care este aria suprafeţei exterioare a „paharului” obţinut?

1. c) Se umple „paharul” cu apă de 8 ori şi se goleşte conţinutul într-un vas cu capacitatea de un litru. Se umple acest vas?

2. Dintr-o foaie de tablă dreptunghiulară cu lungimea de 80 cm şi lăţimea de 60 cm se taie un număr maxim discuri cu raza de 5 cm.

(5p)    a) Care este aria unui disc?

(5p)    b) Câte discuri se obţin?

(5p)    c) Cât la sută din material se pierde?