Varianta 165

Prof: Iuliana Traşcă

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Cel mai mic număr natural din intervalul \((\sqrt{27},\infty )\)este...

(5p)     2. Valoarea lui x pentru care \(x+\sqrt{49}=\sqrt{576}\) este …

(5p)     3. Într-un trapez baza mare are lungimea de 16 cm, iar baza mică are lungimea de 10 cm. Linia  mijlocie are  lungimea de ... cm

(5p)     4. Rezultatul calculului x² -64-(x+8)(x-8)+64 este....

(5p)     5.  Un triunghi ABC are aria 100 cm². Dacă M este mijlocul lui BC, atunci aria triunghiului ABM este....cm²

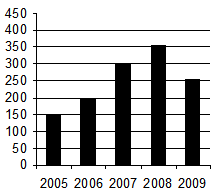
(5p)     6. Diagrama reprezintă numărul de cărţi împrumutate de la o bibliotecă şcolară în ultimii 5 ani. Numărul  de cărţi împrumutate în ultimii cinci ani este...

 SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi,  pe foaia de examen,  piramida triunghuiulară  regulată VABC  şi apotema piramidei VM, \(\text{M}\in \text{BC}\)

   (5p)     2. De ziua onomastică a fiicei sale, tatăl a cumpărat un inel cu o piatră preţioasă de forma unui  paralelipiped dreptunghic, ale cărui feţe au ariile respective: 1 mm²; \(\frac{5}{2}\) mm²; 10 mm². Câte grame cântăreşte piatra, dacă se cunoaşte că un 1 mm³ cântăreşte 0,005 g?

(5p)     3. Mergând cu viteza  constantă de 60 km/h, un automobil parcurge distanţa dinte două  localităţi în  4 ore. Dacă automobilul ar merge cu viteza constantă de 90 km /h în câte minute ar parcurge distanţa ?

4. Fie expresia \(E(x)=\left( \frac{2{{x}^{2}}}{{{x}^{3}}-{{x}^{2}}+x-1}+\frac{-x+{{x}^{2}}}{{{x}^{2}}+1} \right):\frac{{{x}^{2}}}{{{x}^{2}}-1}+\frac{3}{x}\)

(5p)    a) Să se afle valorile lui x pentru care este definită expresia şi să se aducă expresia la  forma cea mai simplă.

(5p)    b) Aflaţi \(x\in \mathbb{Z}\)astfel încât \(E(x+3)\in \mathbb{Z}\)

(5p)     5. Fie \(f:\mathbb{R}\to \mathbb{R}\), f(x)= 3-4x.  Aflaţi a \(\in \mathbb{R}\) ştiind că f(a)=f(-2a+1).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. O grădină are forma ca în figura de mai jos. Cercul de diametru AB=2 m reprezintă un bazin.\(CD\bot EF\), \(CD\cap EF=\left\{ O \right\}\),\(A,B\in \left[ CD \right]\). Figura EOD reprezintă un sfert  de cerc cu raza EO=OD=2 m, iar figura COF reprezintă un sfert de cerc cu raza CO=OF=4 m.

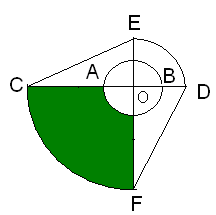
 (5p) a) Să se afle perimetrul grădinii DECF;

 (5p)  b) Să se afle aria grădinii DECF ( exceptând bazinul);

 (5p)  c) Să se afle aria suprafeţei colorate.

2. Un obiect decorativ de sticlă în formă de piramidă triunghiulară regulată are muchia bazei egală cu \(6\sqrt{3}\) dm şi înălţimea egală cu 0,4 m.

(5p)  a) Calculaţi aria totală a obiectului;

(5p)  b) Verificaţi dacă pot intra 36 l de apă în interiorul obiectului;

(5p)  c) La ce distanţa de vârful piramidei trebuie făcută o secţiune paralelă cu baza astfel încât aria secţiunii să fie \(3\sqrt{3}\) dm².