Varianta 171

Prof: Vasile Uleanu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Numărul  0,1(6) scris sub formă de fracţie ordinară ireductibilă este ….

(5p)     2. Dacă \(\frac{4a+3b}{2a+5b}=\frac{3}{4}\) ,  atunci \(\frac{a}{b}=\)  ……          

(5p)     3. Cel mai mare număr  de forma \(\overline{7x3y}\) divizibil cu 45 este …….

(5p)     4. Soluţia reală a ecuaţiei   6 – 3x = x+5 este……

(5p)     5. Raza cercului înscris într-un triunghi echilateral cu înălţimea de 3\(\sqrt{3}\)  cm este …

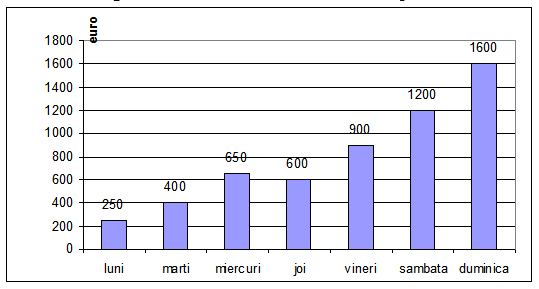
(5p)     6. In diagrama de mai jos sunt reprezentate  vânzările în euro în decursul unei săptămâni la un magazin . Media vânzărilor în această săptămână  este de ….euro

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

 (5p)     1. Desenaţi un paralelipiped dreptunghic ABCDEFGH

(5p)     2. Aflaţi x şi y numere reale ştiind că :    4x² + y²  – 4\(\sqrt{3}\) x + \(2\sqrt{2}\) y = –5

(5p)     3. Aflaţi numerele a şi b ştiind că raportul lor este \(\frac{3}{4}\) iar suma lor este 84.

4. Un trapez ABCD , \(m\left( {\hat{A}} \right)={{90}^{\circ }}\) AB// CD şi CD<AD<BC<AB are perimetrul de 18       cm iar lungimile laturilor sale  sunt exprimate prin 4 numere naturale  consecutive .

(5p)    a) Să se afle aria trapezului ABCD.

(5p)    b) Calculaţi distanţa de la punctul A la latura BC.

(5p)     5. Aflaţi elementele mulţimii A = {  x\(\in \) Z | \(\frac{2x+3}{3x-1}\in \)Z   }                                                                                    

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

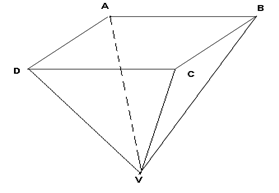
1. Un morar doreşte să-şi confecţioneze din tablă o piesă  în formă de piramidă patrulateră regulată  VABCD  cu vârful V ,  pentru  a o folosi  ca un coş de depozitare a cerealelor  înainte de a fi măcinate . Ştiind că muchia laterală a piramidei are lungimea de \(\sqrt{34}\) dm  , iar diagonala bazei este 60\(\sqrt{2}\) cm , să se afle :

(5p)  a)Aria laterală a   piesei .

 (5p)  b) Volumul  piesei .

(5p)  c) Câte kg de grâu ar putea fi  depozitate în coş  dacă 1 m³  de grâu cântăreşte 1100 kg.

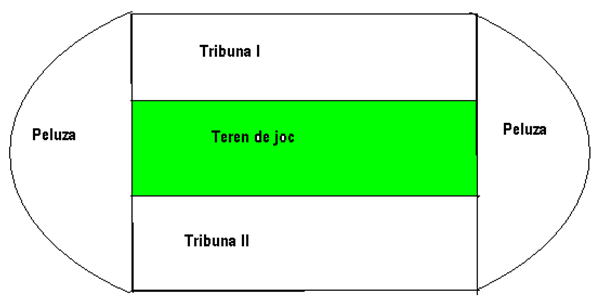
   2. Un stadion de fotbal are forma din figura de mai jos şi este format din teren de joc , 2   tribune şi 2 peluze . Terenul de joc şi cele două  tribune  au formă de dreptunghiuri   care  sunt  congruente iar peluzele sunt două semicercuri fiecare cu  lungimea arcului  de cerc de 105 \(\pi \) m  . Ştiind că lungimea terenului de joc este  120 m  , să se afle :

(5p)  a)Suprafaţa terenului de joc .

(5p)  b) Suprafaţa întregului stadion .

(5p)  c) Ce sumă s-a încasat la un meci de fotbal dacă s-au vândut   1347 bilete la tribuna I-a , 1798 bilete la tribuna a- II-a şi 2683 bilete la peluze ,  iar un   bilet la tribuna I-a costă 15 lei ,la tribuna II-a costă 10 lei , peluză 7 lei  ?