Varianta 172

Prof: Uruc Doina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului: \(300-100:10\) este egal cu ........

(5p)     2. Soluția naturală a ecuației \(2x+5=7\) este .............

(5p)     3. Un pătrat are diagonala de \(3\sqrt{2}\)cm. Perimetrul pătratului este egal cu .......cm.

(5p)     4. Un tetraedru regulat are muchia egală cu 6 cm. Aria totală a tetraedrului este ............\(c{{m}^{2}}\).

(5p)     5. Media aritmetică a numerelor 4 și 12 este egală cu ......... .

(5p)     6. Fie mulțimea \(A=\left\{ x\in \mathbb{R}/x\ge 0 \right\}\). Scrisă sub formă de interval, mulțimea \(A\) este egală cu .............. .

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenați pe foaia de examen o piramidă patrulateră regulată de vârf V și bază ABCD.

(5p)     2. Determinați valoarea minimă a expresiei \(E\left( x \right)=9{{x}^{2}}-6x-3\).

(5p)     3. Rezolvați în \(\mathbb{R}\times \mathbb{R}\) sistemul: \(\left\{ \begin{matrix}  2x+y=0  \\  x+2y=-3  \\ b\end{matrix} \right.\)

 4. Se consideră funcția \(f:\mathbb{R}\to \mathbb{R},f\left( x \right)=2x+1\).

(5p)    a) Reprezentați grafic funcția f.

(5p)    b) Calculați aria triunghiului format de reprezentarea grafică cu axele de coordonate.

(5p)     5. Calculați suma: \(S=\frac{1}{\sqrt{3+2\sqrt{2}}}+\frac{1}{\sqrt{5+2\sqrt{6}}}+\frac{1}{\sqrt{7+2\sqrt{12}}}\)

      SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

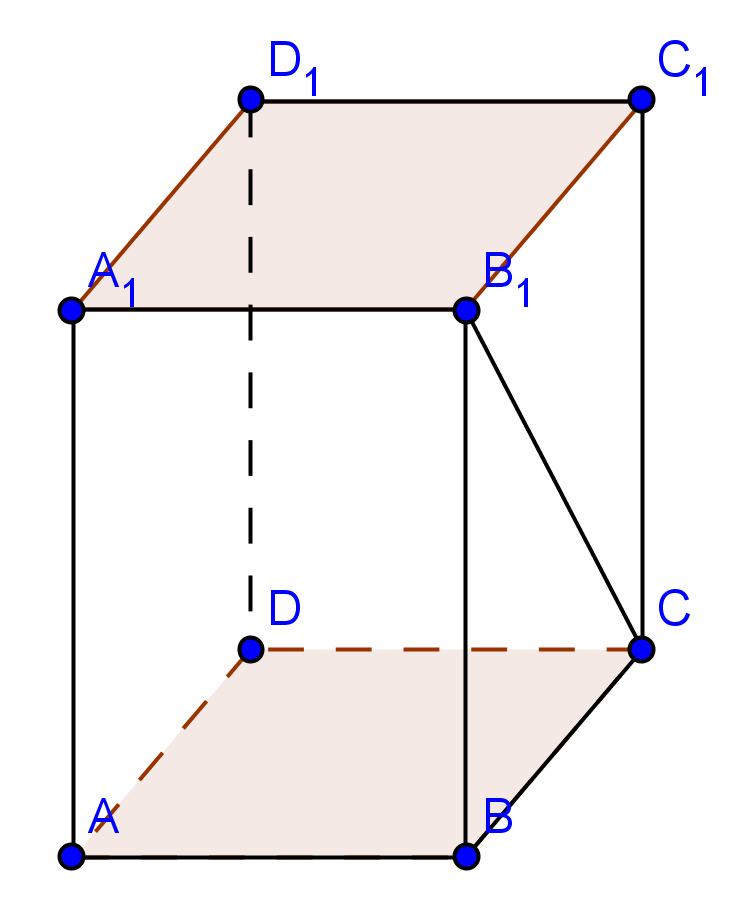
1. O persoană vrea să construiască o sală sub forma unei prisme drepte cu baza pătrat ABCDA₁B₁C₁D₁. Conform proiectului aceasta are aria laterală de 320 m² și volumul de 800 m³.

 (5p)  a) Care sunt dimensiunile sălii?

 (5p)  b) Podeaua trebuie acoperită cu gresie. O cutie cu gresie costă 27,5 lei și conține 6m² de gresie. Știind că de la magazin nu se pot cumpăra decât cutii întregi cu gresie, cât va plăti constructorul pentru pavarea podelei?

 (5p)  c) Beneficiarul dorește ca între B₁ și C să fixeze un panou. Unde trebuie fixat acesta astfel încât distanța dintre A și panou să fie minimă?

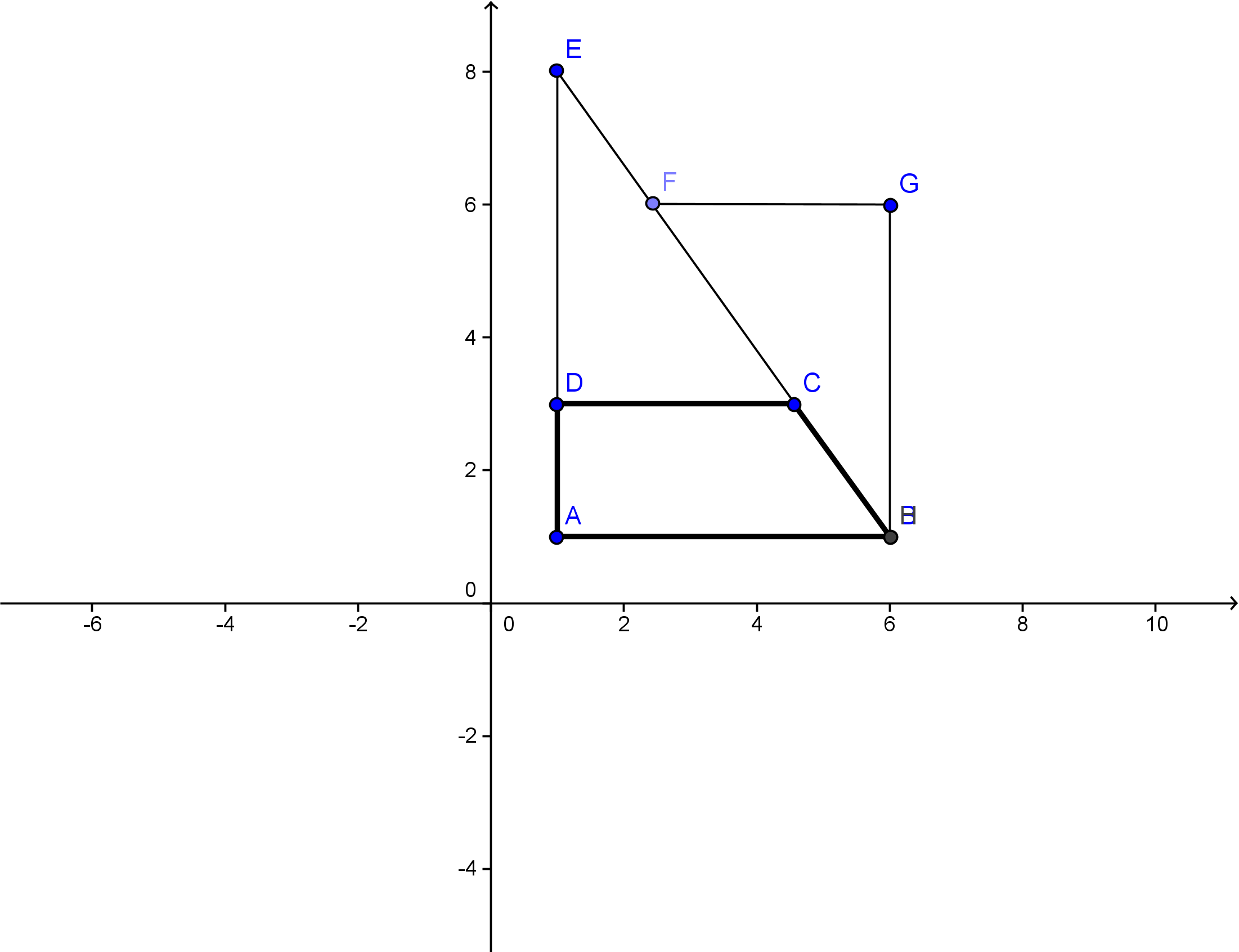
 2. O grădină are forma unui trapez dreptunghic ABCD, \(AB||CD\), \(m\left( \sphericalangle A \right)={{90}^{o}}\), \(m\left( \sphericalangle B \right)={{60}^{o}}\), BC=20m, \(AC\bot BC\), ca în figura alăturată.

(5p)  a) Aproximați suprafața grădinii prin cel mai apropiat număr natural (\(\sqrt{3}\simeq 1,73\)).

(5p)  b) Calculați perimetrul suprafeței \(EDC\).

(5p)  c)Datorită necesității unor construcții suprafața EDC este înlocuită cu un teren BGF așezat ca în figură. Ce distanță este între F și D?