Varianta 173

Prof: Uruc Doina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \({{3}^{0}}+{{3}^{1}}+{{3}^{2}}\) este egal cu ...

(5p)     2. Media geometrică a numerelor 3 și 75 este egală cu ...

(5p)     3. Aria unui dreptunghi cu lungimea de 6 metri și lățimea \(\frac{1}{3}\) din lungime este egală cu ... m².

(5p)     4. Dacă 15 kg de mere costă 30 lei atunci 8,5 kg de mere de același fel vor costa ... lei.

(5p)     5. O piramidă patrulateră regulată are latura bazei de 10 cm și înălțimea de 6 cm. Volumul piramidei este egal cu ... cm³

(5p)     6. Într-o urnă sunt 10 bile albe și 15 bile negre. Probabilitatea ca, extrăgând o bilă, aceasta să fie albă este egală cu ....

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenați pe foaia de examen o piramidă tiunghiulară regulată VABC.

(5p)     2. Să se arate că pentru orice \(x\in \mathbb{R}\backslash \left\{ -1,2 \right\}\) expresia \(E\left( x \right)=\left( \frac{2}{x-2}-\frac{2}{x+1} \right):\frac{-2}{\left( x+1 \right)\left( x-2 \right)}\) este număr întreg.

(5p)     3. După ce s-a scumpit cu 20% un produs costă 60 lei. Cât a costat produsul înainte de scumpire?

 4. Se consideră funcția: \(f:\mathbb{R}\to \mathbb{R},f\left( x \right)=ax+b\)

(5p)    a) Determinați a și b știind că punctele \(A\left( 1,1 \right)\) și \(B\left( 2,0 \right)\) aparțin graficului funcției.

(5p)    b) Pentru \(a=-1\) și \(b=2\) determinați distanța de la punctul de intersecție al axelor de coordonate la dreapta ce reprezintă graficul funcției.

(5p)     5. 5 muncitori pot termina o lucrare în 9 ore. După ce lucrează împreună 3 ore, doi muncitori pleacă. În câte ore vor termina lucrarea muncitorii rămași?

    SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

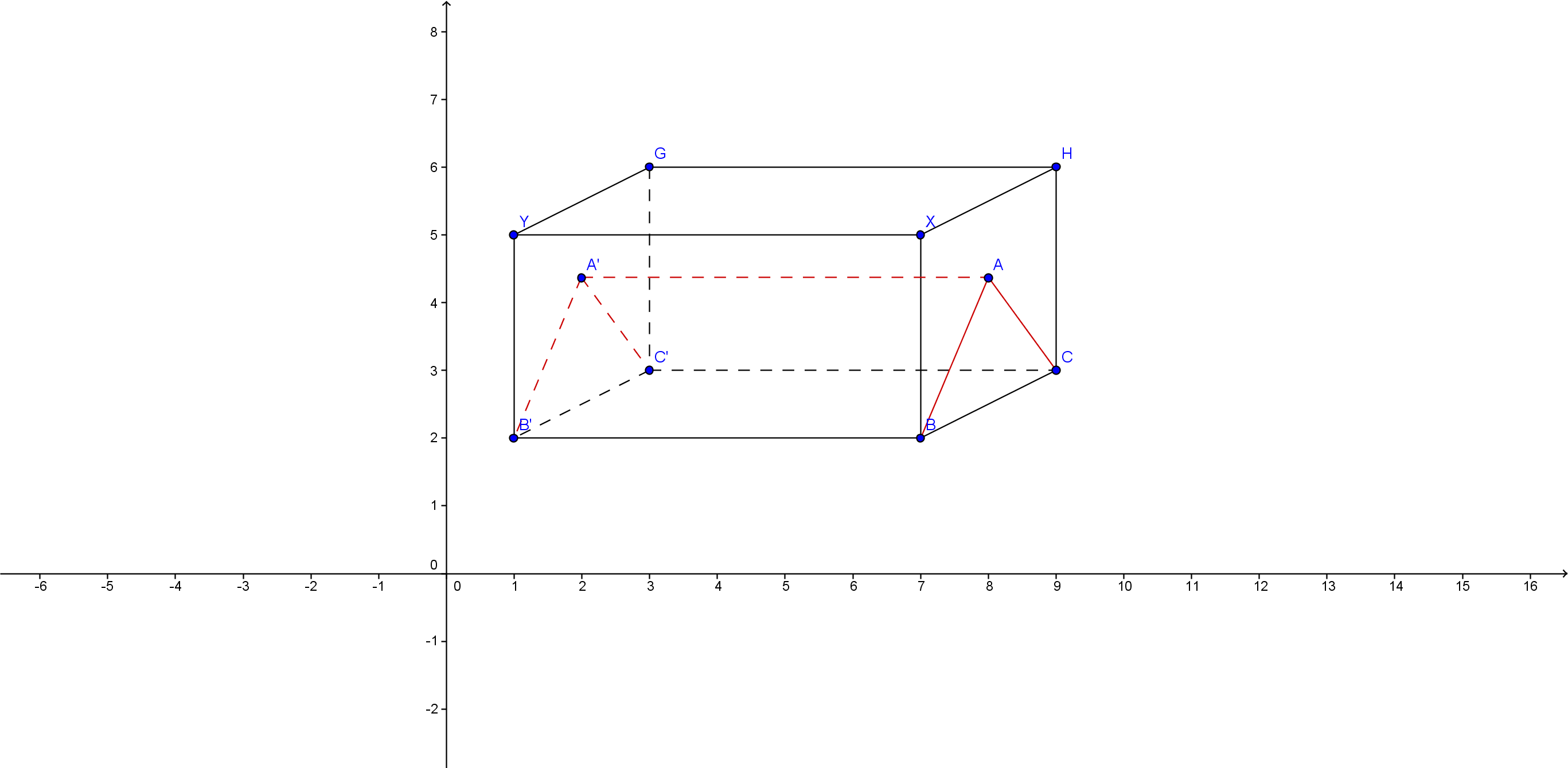
1. Într/un vagon de forma unei prisme patrulatere regulate cu lungimea BB’=10m și înălțimea CH=4m, se introduce o piesă sub formă de prismă triunghiulară regulată ca în figura alăturată.

 (5p)  a) La ce distanță de baza vagonului se află punctul A?

 (5p)  b) Exprimați prin raport procentual raportul dintre volumul piesei și cel al vagonului (\(\sqrt{3}\simeq 1,7\)) 

 (5p)  c) Piesa se acoperă cu o prelată pe părțile care nu sunt în contact cu vagonul. Aflați aria prelatei.

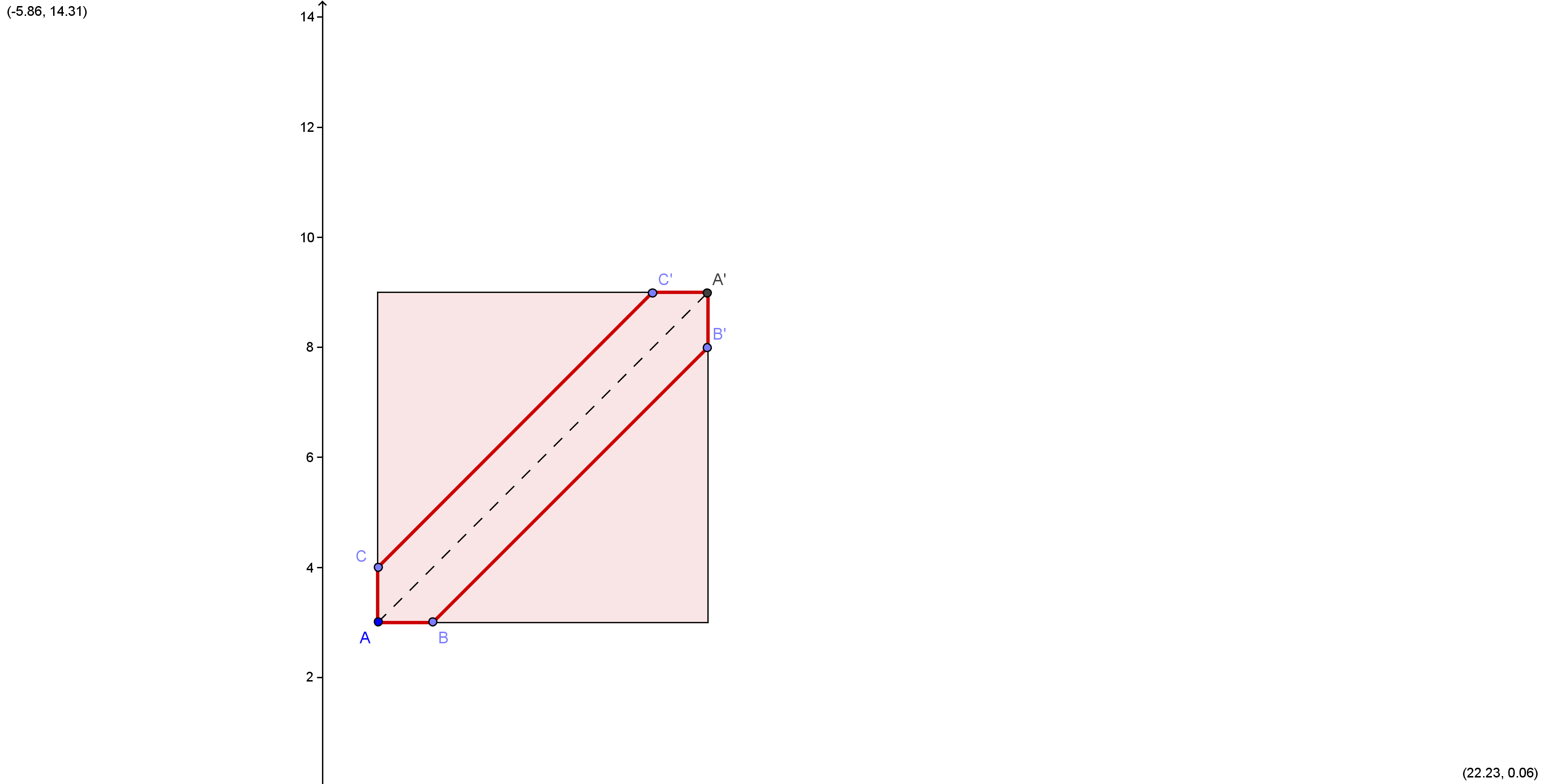
 2. Un adult face 150 pași într-un minut. El parcurge pe diagonala AA’ terenul din figură, în formă de pătrat, în 80 secunde. Lungimea pasului său este egală cu 0,8 metri.

(5p)  a) Care este lungimea laturii terenului?

(5p)  b) Se construiește o alee simetrică față de diagonală, ca în figură, cu lățimea de 2 metri. Care este aria aleei ABB’A’C’C?

(5p)  c) Pe marginea acestei alei se află un copac înalt de 2,40 metri. Andrei observă că umbra proprie are lungimea de 1,20 metri. Știind că înălțimea lui Andrei este de 1,50 metri aflați la ce distanță maximă poate să se așeze faț de copac astfel încât umbra lui să nu o depășească pe cea a copacului?