Varianta 175

Prof: Badea Daniela

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului 324 : 3 este egal cu ........

(5p)     2. Cel mai mare număr întreg mai mic decât  –\(\sqrt{94}\) este .....

(5p)     3. Fie funcţia  \(f:\mathbb{R}\to \mathbb{R},\text{ }f\left( x \right)=2-3x.\)Valoarea funcţiei pentru x = –1 este egală cu ….. 

(5p)     4. Un cerc cu raza 8cm are lungimea egală cu .....π cm.

(5p)     5. Aria laterală a unui cilindru circular drept cu secţiunea axială un pătrat de latură 6 cm  este egală cu ....... cm².

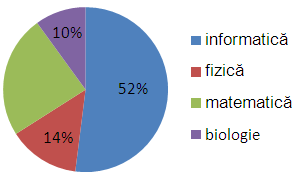
(5p)     6. 50 dintre elevii unei şcoli participă la una dintre olimpiadele şcolare, conform diagramei de mai jos. La olimpiada de matematică participă un număr de ...... elevi.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un trunchi de piramidă triunghiulară regulată MNPQRS.

(5p)     2. Arătaţi că numărul \(N=\frac{2\sqrt{5}+3\sqrt{3}}{2}\) se află în intervalul \(\left( 2\sqrt{5};3\sqrt{3} \right).\)

3. Trei fraţi aveau împreună 130 lei. După ce primul a cheltuit 75% din suma pe care o avea, al doilea a cheltuit două treimi din suma pe care o avea, iar  ultimul a cheltuit două cincimi din suma sa, cei trei fraţi au rămas cu sume egale de bani.

(5p)    a) Aflaţi ce sumă a avut iniţial fiecare dintre fraţi;

(5p)    b) Aflaţi ce sumă a cheltuit fiecare.

4. Fie expresia \(\text{E}\left( x \right)=\frac{x+2}{{{x}^{2}}+1}:\left( \frac{x+3}{4x-4}-\frac{1}{x-1} \right)\cdot \left( 1-\frac{1}{x+2} \right),x\in \mathbb{R}\backslash \left\{ -2;1 \right\}\)

(5p)    a) Arătaţi că \(\text{E}\left( x \right)=\frac{4x+4}{{{x}^{2}}+1};\)

(5p)    b) Rezolvaţi ecuaţia\(\frac{\text{E}\left( x \right)}{4}=\frac{x+1}{2{{x}^{2}}-x-5}.\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Un trunchi de con circular drept are lungimea razei bazei mari egală cu 30 cm, lungimea razei bazei mici egală cu 15 cm şi lungimea generatoarei de 30 cm.

 (5p)   a)Aflaţi măsura unghiului dintre generatoarea trunchiului de con şi planul bazei mari;

 (5p)   b) Calculaţi volumul conului din care provine trunchiul;

 (5p)   c) Calculaţi măsura unghiului sectorului de cerc care reprezintă desfăşurarea suprafeţei laterale a conului din care provine trunchiul de con.

2. În figura de mai jos este reprezentat un suport pentru şerveţele sub forma unui trapez dreptunghic ABCD cu AB || CD, \(m\left( \measuredangle \text{A} \right)=m\left( \measuredangle \text{D} \right)={{90}^{0}},\)AB = 7 cm, CD = 13cm , iar lungimile laturilor BC şi AD sunt direct proporţionale cu numerele 5 şi 4.

(5p)   a) Calculaţi lungimea laturii BC;        

(5p)   b) Calculaţi suprafaţa trapezului;

(5p)   c) Calculaţi distanţa de la punctul D la baza BC a suportului.