Varianta 177

Prof: Boer Elena Milena

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului: \({{2}^{-1}}+\left| 3-7 \right|\) este... .

(5p)     2. Cardinalul mulțimii \(A=\{x\in Z|\left| x+1 \right|\le 3,5\}\) este ... .

(5p)     3. Un elev citește un sfert dintr-o carte în 3 zile. Elevul citește întreaga carte în ... zile.

(5p)     4. Lungimea unui cerc este de \(10\pi \) cm. Lungimea razei lui este egală cu ... cm.

(5p)     5. Volumul unei sfere este de \(36\pi \,c{{m}^{3}}\). Aria sferei este egală cu ... \(c{{m}^{3}}\)

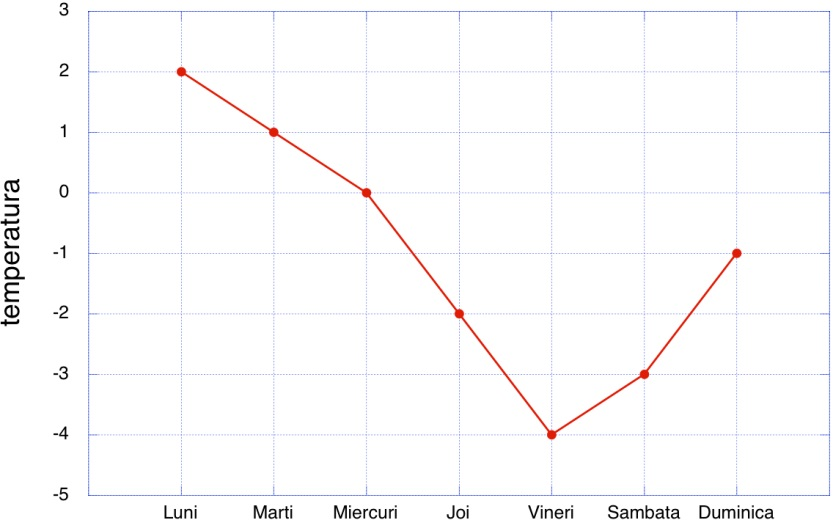
(5p)     6. În diagrama de mai jos, sunt prezentate temperaturile pentru zilele săptămânii 15-21 decembrie 2014 în orașul Brașov. Temperatura medie pentru această săptămână este ... \(^{\circ }C\). 

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

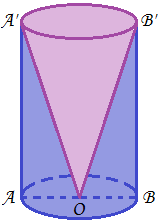
(5p)     1. Desenați pe foaia de examen, un trunchi de piramidă triunghiulară regulată  \(ABCA'B'C'\)

(5p)     2. Se consideră două numere \(a=\sqrt{7}\) și \(b=\sqrt{28}\). Arătați că media geometrică este mai mică decât media lor aritmetică.

(5p)     3. Fie a un număr cuprins între 100 si 200. Împărțind acest număr pe rând la 5, 7 și 10  

se obțin resturile 3, 5 respectiv 8. Aflați numărul.

 4. Se consideră funcția \(f:R\to R,f(x)=-x+4\).

(5p)    a) Verificați dacă punctele A(2, 2) și B(-3, 1) se găsesc pe graficul funcției.

(5p)    b) Aflați distanța de la originea sistemului xOy la graficul funcției.

(5p)     5. Se consideră \(E(x)=\left( \frac{x+2}{{{x}^{2}}-x}+\frac{x-3}{{{x}^{2}}-1}-\frac{x-1}{{{x}^{2}}+x} \right):\frac{{{x}^{2}}+3x+2}{{{x}^{3}}-2{{x}^{2}}+x}\). Arătați că  \(E(x)=\frac{x-1}{x+2}\), pentru orice număr \(x\in R-\{-2,-1,0,1\}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

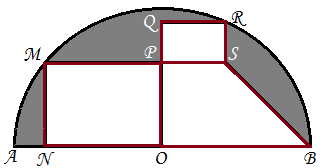
1. Figura 1 reprezintă schema unei baze sportive pentru copii având forma de semicerc. Dreptunghiurile MNOP și PQRS sunt două terenuri de fotbal iar trapezul POBS reprezintă un loc de joacă. Se știe că distanța AO = 10 dam, MN = 6 dam, PS = 6 dam.

 (5p)  a) Determinați distanța NO.

 (5p)  b) Arătați că aria suprafeței hașurate este \(49\,da{{m}^{2}}\) (Considerăm \(\pi =3,14\)).

 (5p)  c) Andrei pornește în linie dreaptă din punctul A către punctul R și apoi în B. Bogdan pornește tot în linie dreaptă din punctul B spre M și apoi spre A. Aflați care copil parcurge un drum mai lung.

 2. Figura 2 reprezintă o piesă având forma unui cilindru circular drept plin cu un miez metalic având forma unui con. Raza și generatarea cilindrului sunt direct proporționale cu 3 și 4  iar aria laterală a acestuia este \(96\pi \,c{{m}^{2}}\).

 (5p)  a) Să se afle volumul cilindrului.

(5p)  b) Care este masa metalului din care este construit miezul metalic. Exprimați rezultatul în kg și aproximați la cel mai apropiat întreg. (Considerăm  \(\rho =7,8\,g/c{{m}^{3}}\)și \(\pi =3,14\) ).

(5p)  c) Cât la sută din volumul cilindrului rămâne după îndepărtarea miezului metalic?