Varianta 178

Prof: Brabeceanu Ionel

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\frac{1}{2}+0,5\)este egal cu….

(5p)     2. Dacă \(\frac{3}{4}=\frac{x}{2}\)atunci \(4\cdot x+4\)este egal cu….

(5p)     3. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R},\text{ }f(x)=2-x.\) Valoarea funcţiei pentru \(x=-2\) este egală cu….

(5p)     4. Triunghiul isoscel \(ABC\) cu \(AB=AC\) are \(m\left( \widehat{A} \right)={{70}^{o}}.\) \(m\left( \widehat{B} \right)=\)….. grade.

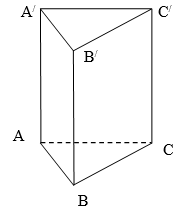
(5p)     5. În figura 1 este reprezentată prisma triunghiulară regulată \(ABC{{A}^{'}}{{B}^{'}}{{C}^{'}}\) cu latura bazei \(AB=6cm\) şi muchia laterală \(A{A}'=8cm\). Lungimea segmentului \(\left[ B{C}' \right]\) este egală cu…...\(cm\).

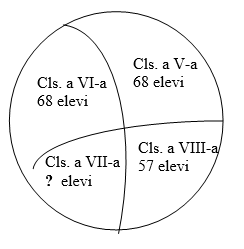
(5p)     6. Diagrama alăturată prezintă repartiţia pe clase a celor 230 elevi de gimnaziu dintr-o şcoală. Câţi elevi sunt în clasa a VII-a.

   SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen o prismă triunghiulară dreaptă \(ABC{{A}^{'}}{{B}^{'}}{{C}^{'}}\) cu baza \(ABC\).

(5p)     2. Arătaţi că numărul \(n=\sqrt{2}-\sqrt{{{\left( -2 \right)}^{2}}}+\left| 1-\sqrt{2} \right|+\left| \sqrt{8}-3 \right|\) este natural.

(5p)     3. Dintr-un grup de copii fetele reprezintă \(\frac{1}{3}\) din numărul băieţilor. Dacă ar mai veni in grup 3 fete şi ar  pleca 7 băieţi atunci numărul fetelor ar fi egal cu numărul băieţilor. Câte fete sunt in grup?

 4. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R},\text{ }f\left( x \right)=-4x+7.\) Într-un sistem de coordonate \(xOy\) reprezentaţi grafic funcţia \(g:\mathbb{R}\to \mathbb{R},\text{ }g\left( x \right)=f\left( 1-\frac{x}{2} \right)\).

(5p)     5. Fie ecuaţia \(3{{x}^{2}}+mx+2=0\) unde \(m\in \mathbb{R}.\)

(5p)    a) Aflaţi valoarea lui \(m\)ştiind că\(-2\)  este soluţie a ecuaţiei.

(5p)    b) Pentru \(m=7\) aflaţi şi cealaltă soluţie a ecuaţiei.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

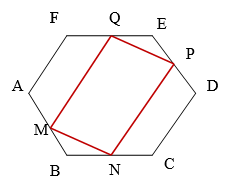
 1. Figura 2 reprezintă modelul unei plăci de gresie în formă de hexagon regulat \(ABCDEF\) cu latura de \(20cm\). Punctele \(M,N,P,Q\) sunt mijloacele segmentelor \(\left[ AB \right],\) \(\left[ BC \right]\), \(\left[ DE \right]\)respectiv\(\left[ EF \right]\).

 (5p)  a) Arătaţi că aria hexagonului \(ABCDEF\) este mai mică decât \(1050c{{m}^{2}}\).

 (5p)  b) Aflaţi aria dreptunghiului \(MNPQ\).

 (5p)  c) Calculaţi lungimea segmentului \(\left[ CQ \right]\).

 2. În figura 3 este reprezentată o piesă din lemn în formă de trunchi de con circular drept cu raza mare de \(10cm\), raza mică de \(6cm\), iar înălţimea de \(24cm\). Din el sunt obţinute prin prelucrare conurile cu vârful \(V\) astfel încât generatoarele unuia sunt în continuarea generatoarelor celuilalt.

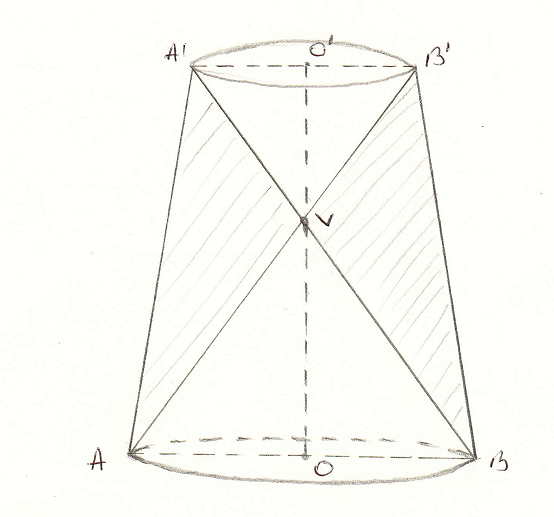
(5p)  a) Aflaţi înălţimea \(V{O}'\) a conului cu raza bazei de \(6cm\).

(5p)  b) Determinaţi lungimea generatoarei conului cu raza bazei de \(10cm\) 

(5p)  c) Stabiliţi volumul de lemn îndepărtat.