Varianta 179

Prof: Brabeceanu Silvia

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\frac{2}{3}+\frac{2}{6}\)este egal cu…..

(5p)     2. Dacă \(x\)este număr real nenul şi \(\frac{5}{3}=\frac{4}{x}\)atunci produsul\(10\cdot x\)este egal cu ……

(5p)     3. Intersecţia reprezentării grafice a funcţiei \(f:\mathbb{R}\to \mathbb{R},\text{ }f\left( x \right)=1-2x\)cu axa \(Oy\)este punctul\(A\left( 0,\cdots  \right)\)

(5p)     4. Un dreptunghi are perimetrul \(40cm\)şi lăţimea\(6cm\) . Lungimea dreptunghiului este egală cu…..cm

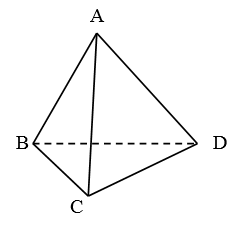
(5p)     5. În figura 1 este reprezentat un tetraedru regulat \(ABCD\). Dacă aria feţei \(ABC\)este \(6\sqrt{3}c{{m}^{2}}\)atunci aria totală a tetraedrului este egală cu…… \(c{{m}^{2}}\).

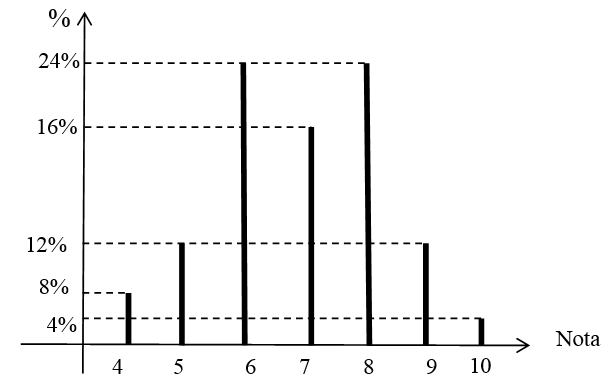
(5p)     6. In graficul de mai jos sunt ilustrate rezultatele la teza de matematică a unei clase a VIII-a.

Ştiind că 4 elevi au luat nota 7 aflaţi câţi elevi sunt în clasă.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen o piramidă triunghiulară \(VABC\)cu vârful \(V\).

(5p)     2. Arătaţi că numărul \(n={{(2\sqrt{3}+1)}^{2}}+{{(\sqrt{3}-2)}^{2}}\)este natural.

(5p)     3. Să se împartă numărul 710 in trei părţi astfel încât prima parte să reprezinte 40% din a doua, iar a doua parte să reprezinte 30% din a treia.

 4. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R},\text{ }f(x)=mx+2m+1;\text{ }m\in \mathbb{R}\) 

(5p)    a). Să se determine \(m\)ştiind că \(A\left( -1,5 \right)\in {{G}_{f}}\).

(5p)   b). Pentru \(m=4\)determinaţi punctul de pe grafic ce are coordonatele egale.

(5p)     5. Se consideră expresia \(E\left( x \right)=\frac{x}{9-{{x}^{2}}}-\frac{x+1}{{{x}^{2}}-6x+9}\)unde \(x\)este număr real, \(x\ne -2\)şi \(x\ne 3\). Arătaţi că \(E\left( x \right)=-\frac{1}{{{\left( x-3 \right)}^{2}}}\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

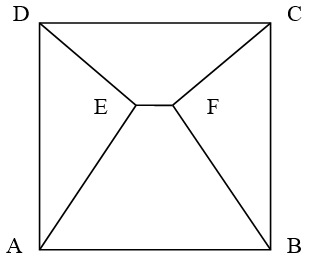
1. Figura 2 reprezintă modelul unei plăci de gresie în formă de pătrat \(ABCD\). Se ştie că \(AE=BF=20cm,\text{ }DE=CF=15cm\)şi \(m\left( \widehat{AED} \right)=m\left( \widehat{BFC} \right)={{90}^{o}}\), aflaţi:

 (5p)  a). Perimetrul pătratului \(ABCD\).

 (5p)  b). Arătaţi că lungimea segmentului \(\left[ EF \right]\)este \(1cm\).

 (5p)  c). Aflaţi aria trapezului isoscel \(ABFE\).

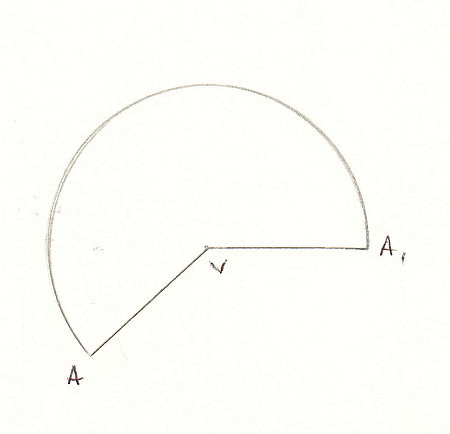
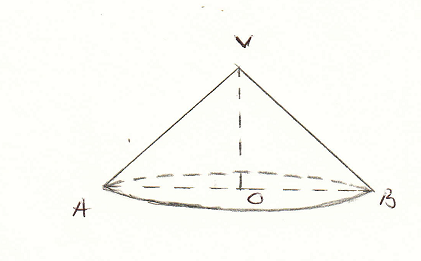
 2. În figura 3 este reprezentat un sector circular din hârtie din care prin înfăşurare se obţine conul circular drept cu vârful în \(V\)şi raza \(R=OA\). Se ştie că \(VA=12cm\)şi \(m\left( \overset\frown{A{{A}_{1}}} \right)={{240}^{o}}\).

(5p)  a). Aflaţi lungimea razei conului.

(5p)  b). Pentru \(R=8cm\)aflaţi aria totală a conului.

(5p)  c). Arătaţi că sinusul unghiului format de generatoarea \(VA\)cu planul bazei conului este mai mic de \(0,75\).