Varianta 180

Prof: Constantin Corina - Carmen

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \({{1}^{2015}}+{{2015}^{3}}:{{2015}^{2}}\) este egal cu ...

(5p)     2. Mulţimea \(\left\{ x\in \mathbb{R}\left| x\le -7 \right. \right\}\cap \mathbb{N}\) este egală cu ...

(5p)     3. Partea întreagă a numărului \(-\sqrt{3}\) este egală cu ...

(5p)     4. Rezultatul calculului \(\sin {{60}^{0}}\cdot tg{{30}^{0}}\) este egal cu ...

(5p)     5. În Figura 1 este reprezentat un cilindru circular drept cu raza de 4 cm şi generatoarea de 5 cm. Volumul cilindrului este egal cu ... \(\pi \) cm³.

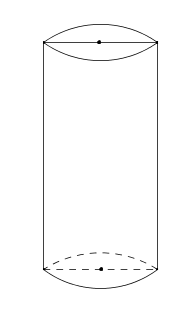
(5p)     6. În graficul de mai jos este prezentată situaţia rezultatelor elevilor claselor a VIII-a la finalul anilor şcolari 2011 – 2014. Diferenţa dintre cea mai mică şi cea mai mare medie este ...

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un tetraedru regulat MATE.

(5p)     2. Calculaţi media geometrică a numerelor reale \(a=\sqrt{7-4\sqrt{3}}\) şi \(b=2+\sqrt{3}\).

(5p)     3. Un autoturism a parcurs o distanţă în trei zile. În prima zi a parcurs o treime din distanţă şi încă 2 km, a doua zi jumătate din distanţă, iar în ultima zi restul de 40 km. Determinaţi distanţa parcursă de autoturism.

 4. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R}\), \(f\left( x \right)=2x-5\).

(5p)    a) Determinaţi numărul real m dacă \(f\left( m-2 \right)=7\).

(5p)    b) Determinaţi aria triunghiului format de graficul funcţiei f cu axele Ox, respectiv Oy ale sistemului de coordonate xOy.

(5p)     5. Se consideră expresia \(E\left( x \right)=\left( \frac{2}{x-3}-\frac{3}{x+3}+\frac{5}{9-{{x}^{2}}} \right):\frac{{{x}^{2}}-8x-20}{{{x}^{2}}-3x}\), unde \(x\in {{\mathbb{R}}^{*}}-\left\{ -3,-2,3,10 \right\}\). Arătaţi că \(E\left( x \right)=\frac{-x}{{{x}^{2}}+5x+6}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. O grădină în formă de disc (ca în Figura 2) are diametrul de 14 m. Grădina este împărţită de aleile AE, OB, OC, OD în 5 părţi, ca în figură, unde O este centrul grădinii. În grădină se plantează pomi fructiferi, trandafiri roşii, portocalii, albi şi galbeni. Suprafeţele în care se plantează trandafirii sunt egale.

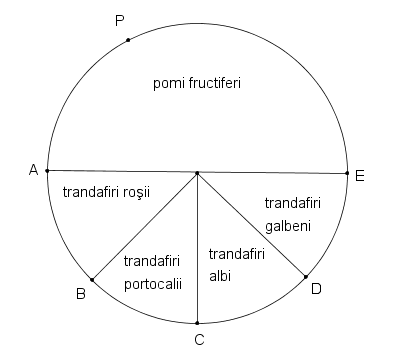
 (5p)  a) Determinaţi suprafaţa plantată cu trandafiri portocalii.

 (5p)  b) Dacă pe aleile late de 0,5 m se pune piatră cubică cu muchia de 10 cm, determinaţi câte pietre cubice sunt necesare pentru a pava aleile.

 (5p)  c) Dacă îngrijitorul grădinii parcurge traseul \(A\to P\to E\to O\to D\to C\to O\to B\to A\), arătaţi că lungimea traseului este mai mică decât 62 m, dacă \(3,14<\pi <3,15\).

 2. Un obiect din lut cu forma de trunchi de con circular drept, ca în Figura 3, are dimensiunile: r = 8 cm, R = 10 cm şi G = 12 cm. Obiectul este umplut cu apă.

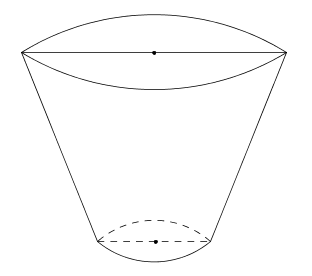
(5p)  a) Arătaţi că în obiect încap aproximativ 3 litri de apă.

(5p)  b) Determinaţi cât la sută din suprafaţa laterală a conului din care provine trunchiul de con reprezintă suprafaţa unui disc cu R = 10 cm (rotunjiţi la cifra unităţilor).

(5p)  c) O furnică parcurge cercul mare al obiectului mergând cu 1 cm/ s. Care este timpul necesar furnicii pentru a străbate distanţa respectivă? (\(\pi \simeq 3,14\))