Varianta 182

Prof: Marcu Daniela

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(10-10:2\)este egal cu........

(5p)     2. Cinci caiete de acelaşi fel costă 4 lei. Zece caiete costă...lei.

(5p)     3. Mulţimea numerelor naturale de două cifre divizibile cu 10 este {…}.

(5p)     4. Un triunghi echilateral are latura de 10 m. Aria triunghiului este egală cu... \({{m}^{2}}\).

(5p)     5. Un glob de sticlă are forma unei sfere având raza de 5 cm. Suprafaţa globului este egală cu... \(\pi c{{m}^{2}}\)

(5p)     6. Rezultatele obţinute de elevii clasei a V a, la testul de admitere în clasa de excelenţă a fost centralizat în tabelul următor :

            Dacă numărul minim de puncte pentru a fi admişi este de 70 de puncte, aflaţi câţi elevi va număra clasa de excelenţă.

  SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen o prismă triunghiulară dreaptă \(ABC{{A}^{'}}B'C'\).

(5p)     2. Calculaţi media geometrică a numerelor reale \(a=3-2\cdot \sqrt{2}\) şi \(b=3+\sqrt{8}\).

(5p)     3. Un tren parcurge un traseu în trei zile. În prima zi trenul a parcurs 50% din lungimea traseului, în a doua zi 30% din lungimea traseului, iar în a treia zi restul de 200 km. Calculaţi lungimea întregului traseu.

 4. Se consideră funcţia : \(f:R\to R,f(x)=2\cdot x-a\), unde a este un număr real.

(5p)    a) Determinaţi numărul real a, ştiind că \(f(0)=-3\).

(5p)    b) Pentru \(a=3\), reprezentaţi grafic funcţia f.

(5p)     5. Se consideră expresia : \(E(x)=\frac{{{x}^{2}}-9}{x+3}+\frac{{{(x+1)}^{2}}-1}{x}\), unde x este un număr real,  \(x\ne 0,x\ne -3\). Arătaţi că \(E(x)-2\cdot x+1=0\), oricare ar fi numărul real x .

        SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

 1. Figura de mai jos, reprezintă schiţa unui teren de joacă sub forma unui trapez bdreptunghic ABED. Se ştie că AD=AB=10 m, BE=20 m, şi \(DC\bot BE,C\in BE\).

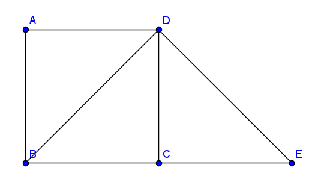
 (5p)  a) Aflaţi suprafaţa terenului de joacă .

 (5p)  b) Arătaţi că triunghiul BDE este dreptunghic isoscel.

 (5p)  c) O fată porneşte din punctul A, şi aleargă până în punctul E, pe traseul \(A\to B\to D\to C\to E\). Arătaţi că distanţa parcursă este mai mică de 45 m.

 2. O foaie de tablă, având formă dreptunghiulară este îndoită sub forma unei suprafeţe cilindrice drepte, ca în figura de mai jos.

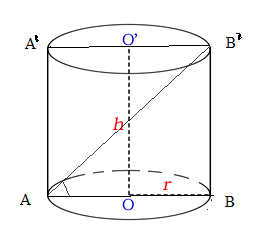
 Se ştie că \(A{{A}^{'}}=100\)cm, \(0A=25\)cm.

(5p)  a) Aflaţi lungimea şi lăţimea foii de tablă.

(5p)  b) Calculaţi sinusul unghiului \({{B}^{'}}AB\).

(5p)  c) Ştiind că \(\pi \cong 3,141...\)arătaţi că suprafaţa foii de tablă, este mai mică de \(1,575\)\({{m}^{2}}\).