Varianta 183

Prof: Marcu Daniela

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(90-45\cdot 2\) este egal cu.........

(5p)     2. Cinci kilograme de portocale costă 15 lei. Trei kilograme de portocale de aceeaşi calitate costă....lei.

(5p)     3. Dacă \(A=\{0,1,2,3,4\}\) şi \(B=\{1,3,5,6,7\}\), atunci mulţimea \(A-B\)este egală cu \(\{...\}\).

(5p)     4. Perimetrul unui triunghi echilateral este de 3 cm. Aria triunghiului echilateral este egală cu.... \(c{{m}^{2}}\).

(5p)     5. Aria unei sfere este egală cu \(4\cdot \pi c{{m}^{2}}\). Volumul sferei este egal cu.... \(c{{m}^{3}}\).

(5p)     6. Notele obţinute de elevii dintr-o şcoală, la evaluarea naţională au fost centralizate în următorul tabel :

              Numărul elevilor care au obţinut note peste 5, este egal cu....

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen, un paralelipiped dreptunghic \(ABCD{{A}^{'}}B'C'{{D}^{'}}\).

(5p)     2. Arătaţi că numărul \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}+\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}\) este un număr natural.

(5p)     3. Un turist, parcurge un traseu de munte în trei zile. În prima zi parcurge 10 km, în a doua zi 40% din lungimea traseului, iar în a treia zi 20% din lungimea traseului. Care este lungimea întregului traseu ?

 4. Se consideră funcţia : \(f:R\to R,f(x)=2\cdot x-3\cdot a\), unde a este un număr real.

(5p)    a) Determinaţi numărul real a, ştiind că \(f(3)=0\).

(5p)    b) Pentru \(a=2\), reprezentaţi grafic funcţia f.

(5p)     5. Se consideră expresia :\(E(x)=(\frac{x-1}{{{x}^{2}}-3\cdot x+2}+\frac{x-2}{{{x}^{2}}-4\cdot x+4}):\frac{2}{x-2}\), unde x este un  număr real,\(x\ne 1,x\ne 2\). Arătaţi că \(E(x)=1\), oricare ar fi numărul real x cu \(x\ne 1,x\ne 2\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. În figura de mai jos, este prezentată o grădină având forma unei suprafeţe dreptunghiulare ABCD, şi suprafaţa de \(1800c{{m}^{2}}\). Grădina este împărţită în trei parcele dreptunghiulare [DPMQ], [PARM], [RBCQ] , având suprafeţele egale. Se ştie că lungimea grădinii este egală cu dublul lăţimii sale.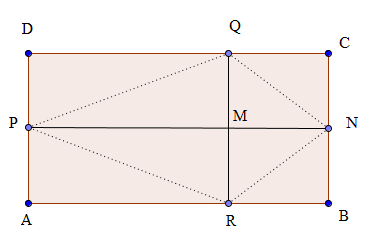

 (5p)  a) Aflaţi suprafaţa unei parcele.

 (5p)  b) Aflaţi lungimea şi lăţimea grădinii .

 (5p)  c) Prelungirea segmentului PM, intersectează latura BC în punctul N. Calculaţi perimetrul patrulaterului PQNR.

 2. Figura de mai jos, reprezintă un trunchi de con circular drept. Se ştie că : \(OA=R=13cm\), \({{O}^{'}}A'=r=10cm\), \(A{{A}^{'}}=g=5cm\).

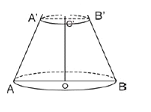
(5p)  a) Calculaţi lungimea înălţimii trunchiului de con.

(5p)  b) Calculaţi volumul trunchiului de con.

 (5p)  c) Aflaţi lungimea generatoarei conului, din care provine trunchiului de con.