Varianta 184

Prof: Marcu Ştefan Florin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\frac{1}{2}+\frac{1}{3}+\frac{1}{6}\)este egal cu........

(5p)     2. Trei kilograme de mere costă 9 lei. Patru kilograme de mere de aceeaşi calitate costă....lei.

(5p)     3. Cel mai mic număr natural de două cifre, care împărţit la 4 dă restul 3, este....

(5p)     4. Aria unui romb cu diagonalele de lungimi 4 cm, respectiv 5 cm este egală cu.... \(c{{m}^{2}}\).

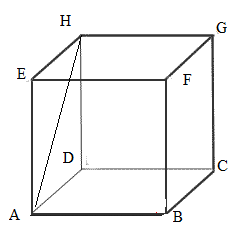
(5p)     5. În figura de mai jos, este reprezentat un cub\(ABCDEFGH\). Măsura unghiului dintre dreptele DC şi AH este egală cu \({{....}^{\circ }}\).

 (5p)     6. Rezultatele obţinute de elevii clasei a VIII a la teza de matematică, au fost  centralizate în următorul tabel :

               Numărul elevilor care au obţinut note cuprinse în intervalul [5,7] este.....

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen, o piramidă patrulateră regulată VABCD .

(5p)     2. Calculaţi raportul dintre media aritmetică şi media geometrică a numerelor : \(a=2+\sqrt{3}\) şi \(b=2-\sqrt{3}\).

(5p)     3. După o reducere cu 10%, o pereche de pantofi costă 180 lei. Aflaţi preţul perechii de pantofi, înainte de reducere.

4. Se consideră funcţia : \(f:R\to R,f(x)=a\cdot x-4,a\ne 0\)

(5p)    a) Aflaţi numărul real a, ştiind că \(f(1)=0\).

(5p)    b) Pentru \(a=4\), reprezentaţi grafic funcţia f.

(5p)     5. Se consideră expresia : \(E(x)=\frac{3\cdot x-9}{{{x}^{2}}-4\cdot x+4}:\frac{{{x}^{2}}-6\cdot x+9}{x-2},x\in R,x\ne 2,x\ne 3\). Arătaţi că : \((x-2)\cdot (x-3)\cdot E(x)=3,\)oricare ar fi numărul real \(x\ne 2,x\ne 3\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

 1. Figura de mai jos, reprezintă schiţa unei grădini . Proprietarul grădinii vrea să măsoare perimetrul ei . Pentru aceasta porneşte din punctul M, şi ajunge tot în M, mergând pe traseul \(M\to A\to N\to B\to P\to C\to Q\to D\to M\). Suprafaţa pătratică ABCD, este plantată cu roşii, iar suprafeţele triunghiulare echilaterale MAD, NAB, PBC, QCD sunt    plantate cu ceapă. Se ştie că \(AB=50m\).

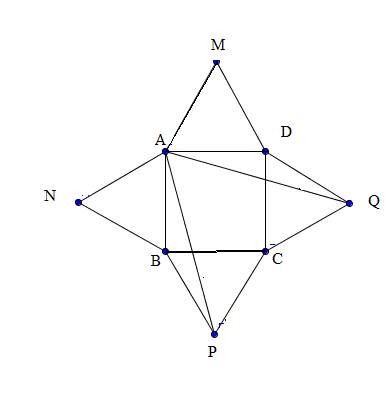
 (5p)  a) Ce distanţă a parcurs proprietarul grădinii ?

 (5p)  b) Calculaţi măsura unghiului PAQ.

 (5p)  c) Arătaţi că, raportul dintre suprafaţa plantată cu roşii, şi cele plantate cu ceapă, este un număr real cuprins în intervalul \((0,55;0,58)\).

2. În figura de mai jos, este reprezentat un con circular drept. Se ştie că triunghiul VAB este echilateral având latura de \(20cm\).

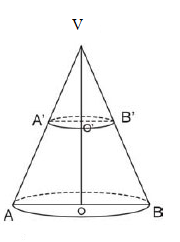
(5p)  a) Aflaţi lungimea înălţimii conului VO.

(5p)  b) Calculaţi volumul conului .

(5p)  c) Conul se secţionează cu un plan paralel cu planul bazei, astfel încât raza secţiunii formate este de \(5cm\). Calculaţi distanţa \(O{{O}^{'}}\).