Varianta 185

Prof: Marcu Ştefan Florin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(30-110:11\)este egal cu.........

(5p)     2. Trei caiete şi două pixuri, costă la fel cu două caiete şi trei pixuri, adică 5 lei. Un pix costă.....lei.

(5p)     3. Cel mai mare număr natural de trei cifre, având produsul cifrelor egal cu 0, este....

(5p)     4. Un pătrat ABCD, are perimetrul de 8 cm. Aria pătratului este egală cu.... \(c{{m}^{2}}\).

(5p)     5. Volumul unei sfere este egal cu \(36\cdot \pi c{{m}^{3}}\). Raza sferei este egală cu....cm.

(5p)     6. Notele obţinute de elevii unei clase la teza de matematică, au fost centralizate în următorul tabel :

              Media clasei este...........

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen, un cub \(ABCD{{A}^{'}}B'C'{{D}^{'}}\).

(5p)     2. Arătaţi că :\(1<\frac{3+\sqrt{2}}{2+\sqrt{3}}<2\).

(5p)     3. După o scumpire cu 10%, preţul unei biciclete este de 770 lei. Aflaţi preţul bicicletei înainte de scumpire .

 4. Se consideră funcţia : \(f:R\to R,f(x)=a\cdot x+b,a,b\in R,a\ne 0\).

(5p)    a) Aflaţi numerele reale a şi b, ştiind că \(f(0)=1\) şi \(f(1)=2\).

(5p)    b) Pentru \(a=b=1\), reprezentaţi grafic funcţia f.

(5p)     5. Se consideră expresia : \(E(x)=\frac{{{x}^{2}}-2\cdot x+1}{{{x}^{2}}-1}+\frac{2\cdot x+4}{{{x}^{2}}+3\cdot x+2},x\in R,x\ne -2,x\ne -1,x\ne 1\). Arătaţi că \(E(x)=1\), oricare ar fi numărul real x cu \(x\ne -2,x\ne -1,x\ne 1\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Fie ABCD un paralelogram, cu \(AB=10m,BC=10\cdot \sqrt{3}m\) şi \(m(\measuredangle ABC)={{60}^{\circ }}\). Ducem \(BM\bot AD\)şi \(DN\bot BC,M\in AD,N\in BC\).

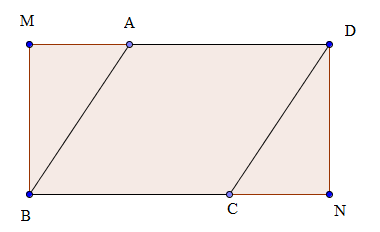
 (5p)  a) Calculaţi aria paralelogramului ABCD.

 (5p)  b) Arătaţi că MBND este dreptunghi.

 (5p)  c) Arătaţi că\(MN<24m\).

 2. Figura de mai jos, reprezintă un con circular drept, cu \(VA=VB=10cm,VO=OA\).

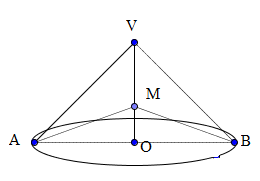
(5p)  a) Calculaţi volumul conului.

(5p)  b) Aflaţi măsura unghiului AVB.

(5p)  c) Conul se secţionează cu un plan paralel cu planul bazei, dus prin punctul M de intersecţie a medianelor triunghiului VAB. Aflaţi raza secţiunii.