Varianta 187

Prof: Marcu Tamara

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(24:4-5:5\) este.....................

(5p)     2. Soluţia ecuaţiei \(2x-1=5\)este......................

(5p)     3. Dintre numerele 9991, 1089 şi 1999, numărul divizibil cu 9 este..............

(5p)     4. Măsura unghiului format de o diagonală a unui pătrat cu una din laturi este egal   cu..............

(5p)     5. Volumul sferei cu raza de 3 cm este egal cu........ \(c{{m}^{3}}\).

(5p)     6. Rezultatele unui test la matematică sunt prezentate în următorul tabel:

            Numărul elevilor care a obţinut note mai mari decât 7 este egal cu...................              

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen, un con.

(5p)     2. Calculaţi suma nr. a şi b unde \(a=\frac{11}{2\sqrt{3}-1}\)şi \(b=1-\sqrt{24}:\sqrt{2}\)

(5p)     3. Media aritmetică a trei numere este 9. Ştiind că două dintre ele sunt 8 şi 3 aflaţi cel de-al treilea număr.

4. Fie funcţia \(f:\mathbb{R}\to \mathbb{R},f\left( x \right)=-2x+1.\)

(5p)          a) Aflaţi \(a\in \mathbb{R}\), astfel încât punctul \(A(1;a-1)\) să aparţină reprezentării geometrice a graficului funcţiei f.

(5p)          b) Reprezentaţi grafic funcţia.

(5p)     5. Pentru \(x\ne y\) şi \(x\ne -y\), efectuaţi: \(\frac{{{x}^{2}}+xy}{x-y}:(x+y)=\)

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Într-un cilindru, raza şi generatoarea sunt direct proporţionale cu 5 şi 6 iar suma lor este 22 dm.

 (5p)  a) Determinaţi raza şi generatoarea cilindrului.

 (5p)  b) Dacă R= 10 dm şi G= 12 dm, calculaţi aria secţiunii axiale.

 (5p)  c) Aflaţi volumul cilindrului.           

2. O piesă de puzzle se obţine prin decuparea din pătratul de carton ABCD a triunghiului echilateral ABE. Lungimea laturii pătratului este de 4 cm. Calculaţi:

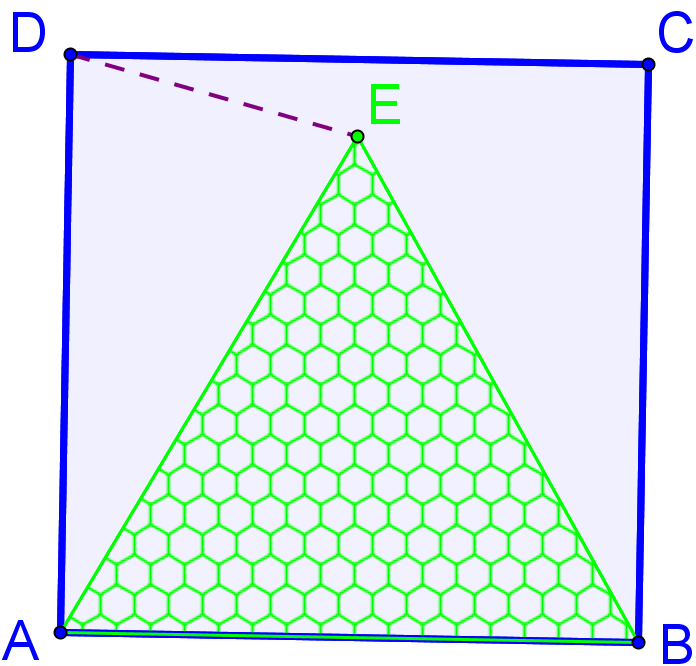
(5p)   a) aria triunghiului îndepărtat;

(5p)   b) măsurile unghiurilor DAE şi ADE;

(5p)   c) distanţa de la punctul D la AE.