Varianta 190

Prof: Mocanu Ana-Gabriela

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1.Rezultatul calculului \(\frac{1}{2}+\frac{1}{2}:\frac{1}{2}\) este egal cu....

(5p)     2. Un bazin poate fi umplut de 6 robinete în 40 minute.Pentru a umple bazinul în două ore ar fi nevoie de ...robinete.

(5p)     3.Scrisă sub formă de interval mulţimea A=\(\left\{ x\in \mathbb{R}/x\ge 3 \right\}\)este egală cu....

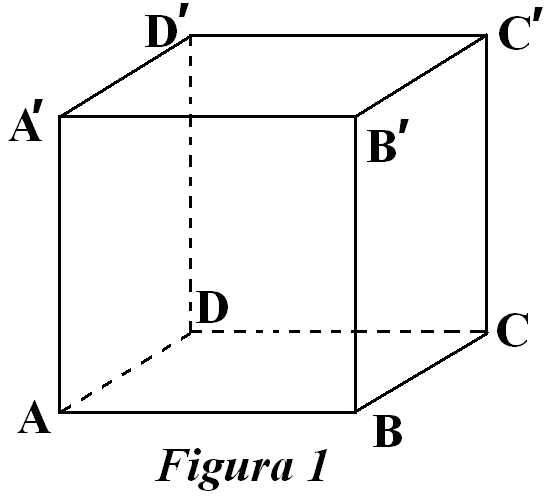
(5p)     4. \(ABCDA\prime B\prime C\prime D\prime \)din\(figura\) \(1\). este un cub.Măsura unghiului dintre dreptele \(AD\prime \) şi \(DC\prime \) este egală cu ...\({}^\circ \).   

(5p)     5.Lungimea liniei mijlocii a unui trapez este egală cu 8 cm, iar lungimea înălţimii este de 7cm.Aria trapezului este egală cu...\(c{{m}^{2}}\).

 (5p)    6. Rezultatele elevilor unei clase a VIII-a la examenul de Evaluare Naţională sunt prezentate pe tranşe de medii în tabelul de mai jos.Procentul elevilor care au obţinut cel puţin nota 5 ,este gal cu...%.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi un trunchi de piramidă triunghiulară regulată \(ABCA\prime B\prime C\prime \).

(5p)     2. Calculaţi \(\frac{1}{\sqrt{3}-\sqrt{2}}-(\sqrt{3}-\sqrt{2}).\)

(5p)     3. Un turist a parcurs un traseu în doua zile .În prima zi a parcurs 40 % din lungimea traseului  şi încă 6km,iar în a doua zi restul de 120 km.Calculaţi lungimea întregului traseu.

 4. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R}\),\(f(x)=-\frac{4}{3}x+a\),unde \(a\)este un număr real.

(5p)    a)Determinaţi numărul real \(a\),ştiind că \(f(0)=4.\)

(5p)    b)Pentru \(a\)=4,calculaţi lungimea segmentului \(AB\), unde \(A\) şi \(B\) sunt punctele de intersecţie  a graficului funcţiei \(f\)cu axele \(Ox\) ,respectiv \(Oy\) ale sistemului de coordonate \(xOy\).

(5p)     5. Se consideră expresia \(E(x)=\frac{{{(x+1)}^{2}}-4}{x}:\frac{{{x}^{2}}-x}{{{x}^{3}}}\) ,unde \(x\) este număr real, \(x\ne 0\)şi \(x\ne 1\).Determinaţi numărul real m,\(m\ne 0\) şi \(m\ne 1\),ştiind că \(E(m)=4\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Figura 2 este schiţa unei grădini în formă de dreptunghi \(ABCD\),iar \(AC,BE\)şi \(DF\),(\(BE\bot AC,DF\bot AC\)) reprezintă garduri ce separă diferite parcele din grădină.\(AE=5m\)şi \(EC=15m\). Pe suprafeţele \(AEB\) şi \(CFD\) sunt cultivate flori.

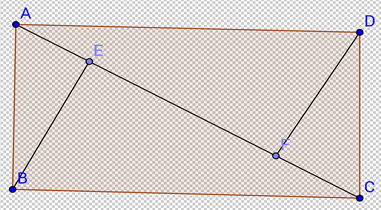
 (5p)  a)Arătaţi că \(AB=10m\)şi \(BC=10\sqrt{3}m\).

 (5p)  b)Arătaţi că suprafaţa grădinii este mai mică decât 2 ari.Se consideră cunoscut faptul că \(1,73<\sqrt{3}<1,74\).

 (5p)  c)Aflaţi cât la sută din suprafaţa grădinii este cultivată cu flori.

 2. În Figura 3. este reprezentat un con circular drept cu generatoarea VA=20 cm.Segmentul AB=24cm este diametru al bazei conului.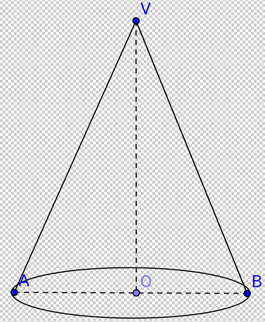

(5p)  a)Arătaţi că volumul conului circular drept  este egal cu 768\(\pi \)\(c{{m}^{3}}\).

(5p)  b)Conul se secţionează cu un plan paralel cu baza astfel încât lungimea secţiunii formate este egală cu \(6\pi \)cm.Determinaţi distanţa de la punctul V la planul de secţiune.

(5p)  c)Calculaţi aria laterală a trunchiului de con circular drept obţinut în urma secţionării.