Varianta 193

Prof: Păcurar Cornel-Cosmin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(10-10:2\) este egal cu... .

(5p)     2. Trei kilograme de mere costă \(75\) de lei.Două kilograme de mere de aceeași calitate costă......lei.

(5p)     3. Cel mai mic număr întreg de două cifre este egal cu... .

(5p)     4. Perimetrul pătratului care are aria egală cu \(25\) \(c{{m}^{2}}\)este egal cu.... \(cm\).

(5p)     5. O sferă de rază \(3cm\).Aria sferei este egală cu ... \(\pi c{{m}^{2}}\)

(5p)     6. În tabelul de mai jos este reprezentată o dependență funcțională.

Numărul real \(m\) este egal cu ... .

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenați, pe foaia de examen, un cilindru circular drept.

(5p)     2. Arătați că \(\frac{2}{\sqrt{6}-2}-\sqrt{6}=2\).

(5p)     3. Prețul unui televizor este de \(2000\) de lei.Aflați prețul televizorului după două reduceri succesive de preț, prima de \(10%\) iar a doua de \(5%\).

 4. Se consideră funcția \(f:\mathbb{R}\to \mathbb{R},\)\(f(x)=ax+2\), unde \(a\) este un număr real.

(5p)    a)Determinați numărul real \(a\), știind că \(f(-2)=0\).

(5p)    b)Pentru \(a=1\), arătați că triunghiul OAB este isoscel, unde A și B sunt punctele de intersecție a graficului funcției \(f\) cu axele \(Ox\), respectiv \(Oy\) ale sistemului de coordonate \(xOy\).

(5p)     5.Se consideră expresia  \(E(x)=\frac{{{\left( x+2 \right)}^{2}}-9}{x}:\frac{{{x}^{2}}-x}{{{x}^{2}}}\), unde \(x\) este un număr real, \(x\ne 0\) și \(x\ne 1\).Determinați numărul real \(m,\)\(m\ne 0\) și \(m\ne 1\), știind că \(E(m)=7\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. \(Figura2\) este schița unui parc în formă de dreptunghi ABCD străbătut de aleea în formă de paralelogram\(MDNB\). Se știe că\(AD=400m\) , \(AB=100m\)și \(MD=BN=5m\).

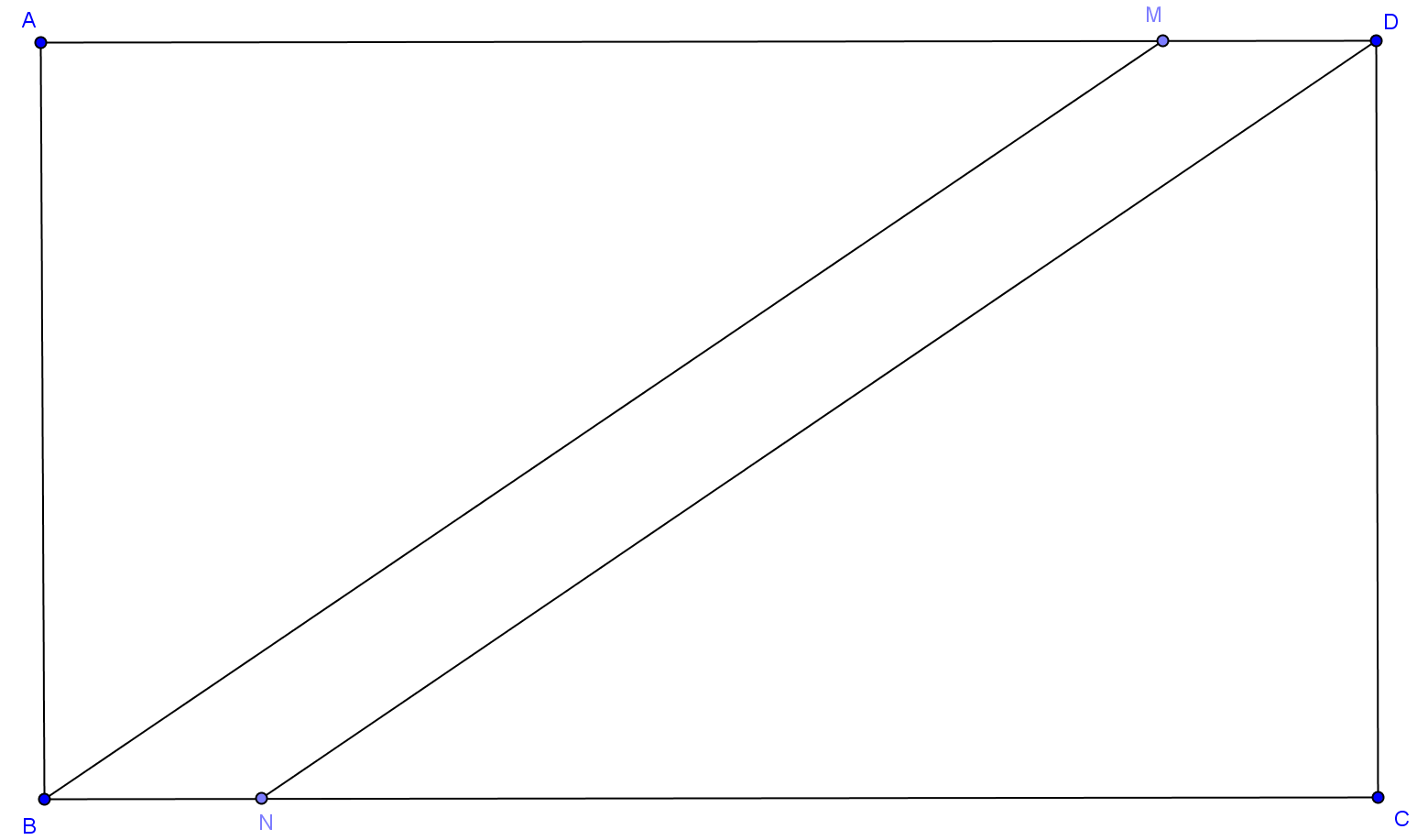
 (5p)  a)Aflați aria dreptunghiului ABCD.

 (5p)  b)Aflați aria paralelogramului \(MDNB\).

 (5p)  c)Aflați distanța cea mai mică pe care o parcurge un biciclist care vrea sa traverseze parcul prin aleea \(MDNB\).

 2. În \(Figura3\)este reprezentat un con circular drept cu înălțimea \(VO\),\(VO=6cm\).Segmentul \(AB\)este diametru al bazei conului și \(VA=10cm\).

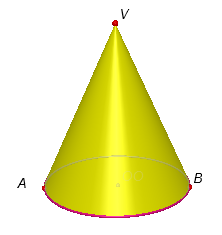
(5p)  a)Arătați că volumul conului circular drept este egal cu \(128\pi \)\(c{{m}^{3}}\).

(5p)  b)Calculați valoarea sinusului unghiului format de generatoarea conului cu planul bazei.

(5p)  c)Conul se secționează cu un plan paralel cu planul bazei astfel încât aria secțiunii formate este egală cu \(4\pi c{{m}^{2}}\).Determinați distanța de la punctul \(V\) la planul de secțiune.