Varianta 194

Prof: Păcurar Cornel-Cosmin

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Numărul de 3 ori mai mare decât 8 este egal cu... .

(5p)     2. Soluția ecuației \(2x-3=13\)este egală cu... .

(5p)     3.Dacă \(A=\left\{ 1,2,3,4 \right\}\)și \(B=\left\{ 3,4,5,6 \right\}\),atunci mulțimea \(A\cup B\)este egală cu\(\left\{ ............. \right\}\)

(5p)     4. Rombul \(ABCD\)are \(AC=4cm\)și \(BD=6cm\) atunci aria rombului \(ABCD\) este egală cu ... \(c{{m}^{2}}\)

(5p)     5.În \(Figura1\)este reprezentat un paralelipiped dreptunghic \(ABCDEFGH\)în care \(AB=6cm,BC=4cm\) și \(BF=5cm\).Aria totală a paralelipipedului \(ABCDEFGH\)este egală cu .... \(c{{m}^{2}}\).

(5p)     6. În tabelul de mai jos este prezentată repartiția elevilor unei clase,în funcție de notele obținute la teza la matematică pe semestrul I.

Media clasei la această teză este egală cu .... .

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenați și notați o sferă de centru O și rază R.

(5p)     2. Calculați media geometrică a numerelor \(x=2\left( 7-\sqrt{13} \right)-7+\sqrt{13}\)și \(y=\frac{36}{7-\sqrt{13}}\).

(5p)     3. Un autoturism a parcurs un traseu în două zile.În prima zi autoturismul a parcurs \(40%\)din lungimea traseului, iar în a doua zi autoturismul a parcurs restul de 300 km.Calculați lungimea întregului traseu.

 4. Se consideră funcția \(f:\mathbb{R}\to \mathbb{R},f(x)=x+3.\)

(5p)    a)Calculați \(f(-3)+f(0).\)

(5p)    b)Reprezentați grafic funcția  într-un sistem de coordonate \(xOy.\)

(5p)     5. Se consideră expresia \(E(x)=\left( \frac{{{\left( x+3 \right)}^{2}}}{{{x}^{2}}+9}-1 \right):\frac{x}{{{x}^{2}}+9},\)unde \(x\) este număr real, \(x\ne 0.\) Arătați că \(E(x)=6\) pentru orice număr real \(x,x\ne 0.\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

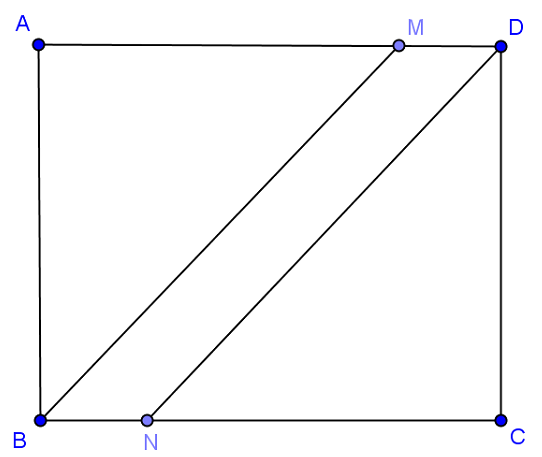
1. \(Figura2\) este schița unui parc în formă de pătrat ABCD străbătut de aleea în formă de paralelogram\(MDNB\). Se știe că \(AB=400m\)și\(MD=BN=20m\).

 (5p)  a)Aflați aria pătratului ABCD.

 (5p)  b)Aflați perimetrul paralelogramului \(MDNB\).

 (5p)  c)Aflați distanța cea mai mare pe care o parcurge un biciclist care vrea sa traverseze în linie dreaptă parcul prin aleea \(MDNB\).

2. În \(Figura3\)este reprezentat un cilindru circular drept care are secțiunea axială dreptunghiul ABCD,O este mijlocul lui \(\left[ AB \right]\)iar Q este mijlocul lui \(\left[ DC \right]\).Se știe că \(AB=8cm\) și \(OQ=9cm\).

(5p)  a)Arătați că volumul cilindrului circular drept este egal cu \(144\pi c{{m}^{3}}\).

(5p)  b)Arătați că aria totală a cilindrului circular drept este egală cu\(104\pi c{{m}^{2}}\).

(5p)  c)Aflați valoarea sinusului dintre AC și planul bazei.