Varianta 198

Prof: Pisică Lăcrămioara

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\sqrt{12}\cdot \sqrt{3}-3\sqrt{3}:\sqrt{3}\) este egal cu ... .

(5p)     2. Dacă 8 pixuri costă 10 lei atunci cu 7,50 lei putem cumpăra ... pixuri de același fel .

(5p)     3. Mulțimea \(A=\left\{ x\in \mathbb{R}|2x-1\le 3 \right\}\), scrisă sub formă de interval, este egală cu ... .

(5p)     4. Aria unui disc ce are diametrul de 8 cm este egală cu ... cm² .

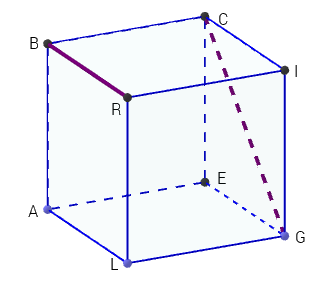
(5p)     5. În figura 1 este reprezentat cubul ALGEBRIC . Măsura unghiului format de dreptele BR și CG este egală cu ...\({}^\circ \).

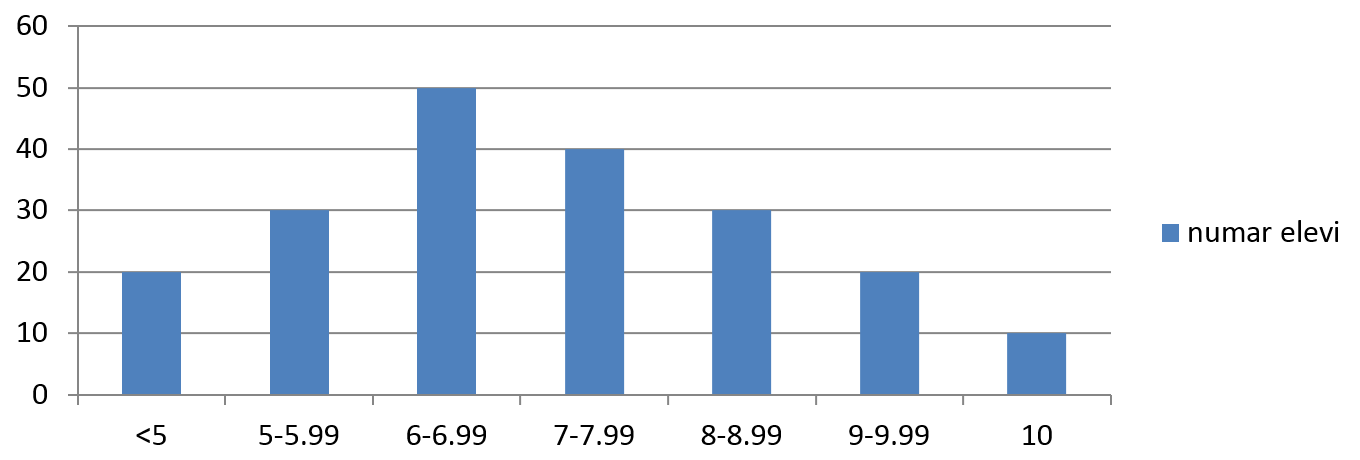
(5p)     6. În graficul de mai jos este reprezentată repartiția elevilor claselor a VIII-a a unei școli după media de admitere.

Numărul elevilor ce au absolvit clasa a VIII-a este egal cu ... .

      SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenați , pe foaia de examen , prisma triunghiulară regulată BRASOV .

(5p)     2. O bluză ce costa 150 de lei se scumpește cu 18 lei. Cu ce procent s-a modificat prețul bluzei ?

(5p)     3. În vederea realizării unui proiect elevii claselor a VIII-a se grupează astfel : un sfert din ei vor culege datele necesare proiectului ; un sfert din restul elevilor și încă doi vor realiza testele de laborator iar restul de 7 elevi se vor ocupa de  tehnoredactare . Câți elevi participă la acest proiect ?

 4. Considerăm expresia \(E(x)=\left( \frac{x}{{{x}^{2}}-x-6}-\frac{3}{{{x}^{3}}-3{{x}^{2}}-4x+12} \right):\frac{x+1}{{{x}^{2}}-4}\) , unde \(x\in \mathbb{R}\backslash \left\{ -2,-1,2,3 \right\}\)

(5p)    a) Determinați numerele întregi a , b , c știind că \({{x}^{3}}-3{{x}^{2}}-4x+12=(x+a)(x+b)(x+c)\)

(5p)    b) Arătați că \(E(x)=1\) pentru orice \(x\in \mathbb{R}\backslash \left\{ -2,-1,2,3 \right\}\)

(5p)     5. Considerând funcțiile \(f,g:\mathbb{R}\to \mathbb{R}\) , \(f(x)=2x+1\) și \(g(x)=3x-1\) , determinați coordonatele punctului de intersecție a celor două grafice .

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. În figura 2 este reprezentat schematic un parc . ABCD este un trapez cu \(AB=36\) dam , \(CD=24\) dam și înălțimea egală cu \(15\sqrt{3}\) dam , \(AC\bigcap BD=\left\{ O \right\}\), iar triunghiurile ABE și DCF sunt echilaterale .

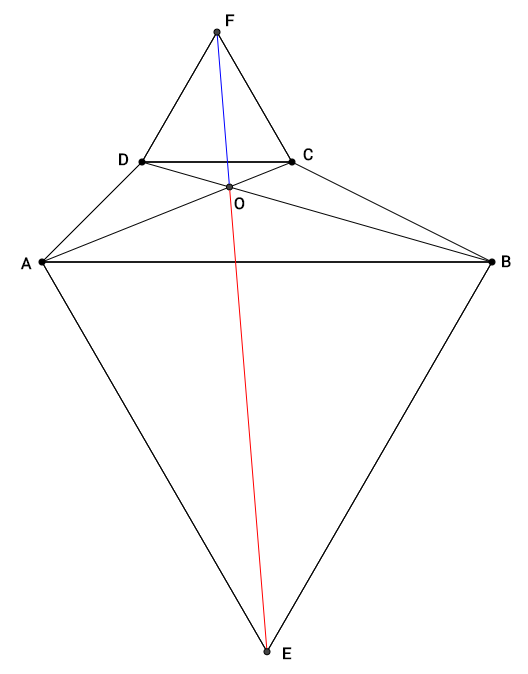
 (5p)  a) Arătați că suprafața parcului are mai mult de 15 hectare . (\(\sqrt{3}\approx 1,73\))

 (5p)  b) Demonstrați că triunghiurile AOE și COF sunt asemenea .

 (5p)  c) Administratorii parcului vor să construiască o pistă pentru biciclete care să unească punctele E și F . Arătați că această pistă va trece și prin punctul O .

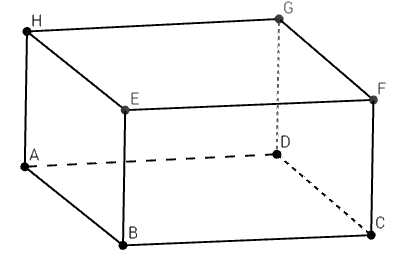
2. În figura 3 este reprezentat un recipient de înghețată ce are forma unui paralelipiped dreptunghic ABCDEFGH cu dimensiunile \(AB=16\) cm , \(BC=12\) cm și \(AE=10\) cm .

(5p)  a) Arătați că în recipient încap mai puțin de 2 litri de înghețată .

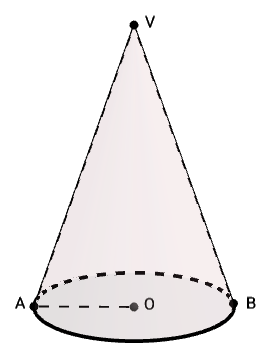
(5p)  b) Turnăm înghețata în conuri confecționate din foi de napolitană cu raza de 2 cm și înălțimea de 9 cm ( figura 4 ) . Arătați că se pot umple 50 de astfel de conuri cu înghețata din recipient .   (\(\pi \approx 3,14\))

(5p)  c) Determinați sinusul unghiului format de două generatoare diametral opuse ale conului reprezentat în figura 4 .