Varianta 199

Prof: Pisică Lăcrămioara.

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(2015:\left( 2\cdot {{10}^{3}}+{{2}^{4}}-1 \right)-{{2015}^{0}}\) este egal cu .. .

(5p)     2. Cel mai mic număr natural de trei cifre care împărțit la 15 dă restul cel mai mare posibil, este egal cu ... .

(5p)     3. 35% din 1 km este egal cu ... m

(5p)     4. Un triunghi dreptunghic isoscel cu mediana de 6 cm are aria egală cu ... cm² .

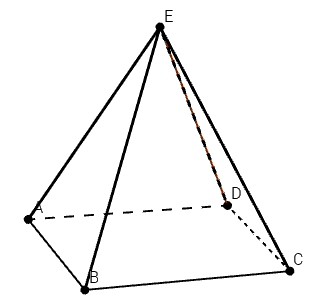
(5p)     5. În figura 1 este reprezentată o piramidă patulateră regulată cu toate muchiile congruente . Dacă perimetrul bazei este de 24 cm atunci aria laterală a piramidei este egală cu ... cm² .

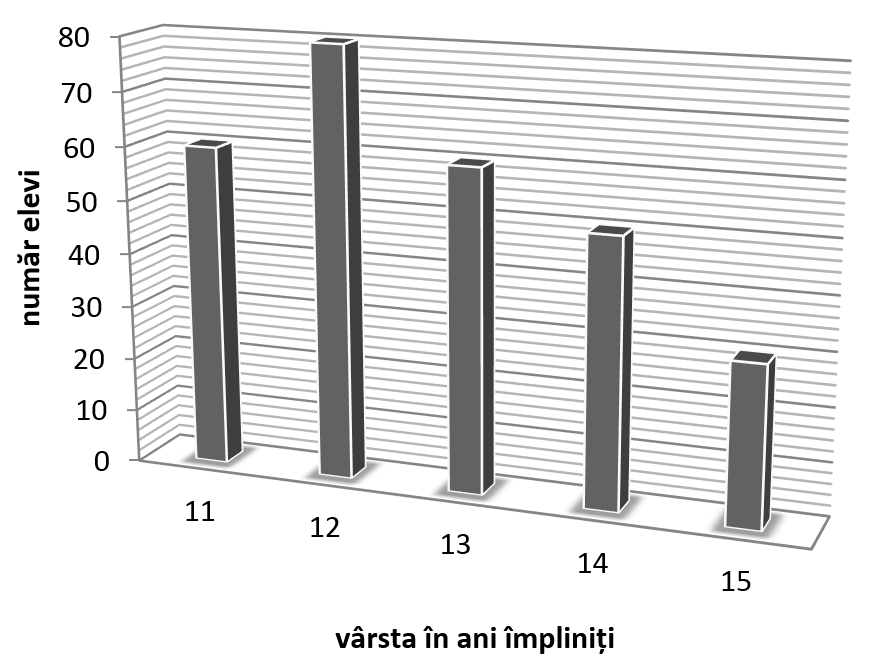
(5p)     6. În graficul de mai jos este reprezentat numărul elevilor dintr-o școală , pe grupe de vârstă .

Numărul elevilor din școală ce nu au împlinit încă 14 ani este egal cu ... .

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenați , pe foaia de examen , piramida patrulateră PARIS .

(5p)     2. Fie numerele \(a=\frac{7}{5-\sqrt{18}}+\sqrt{{{\left( 3\sqrt{2}-5 \right)}^{2}}}\) și \(b=6:\sqrt{3}:\sqrt{3}\) . Arătați că \(a:b-1\) este pătrat perfect .

(5p)     3. La un concurs se acordă 10 puncte pentru o problemă rezolvată corect și se penalizează cu 5 puncte pentru o problemă greșită . Un elev a avut de rezolvat 20 de probleme și a primit 110 puncte . Câte probleme a rezolvat greșit ?

 4. Fie funcția \(f:\mathbb{R}\to \mathbb{R}\) , \(f(x)=ax+1\) .

(5p)    a) Determinați valoarea parametrului natural a știind că punctul \(M(a,2)\) aparține graficului funcției  f .

(5p)    b) Știind că \(a=1\) și notând cu A și B punctele de intersecție a graficului funcției  f cu axele Ox și Oy ale sistemului de coordonate xOy și cu C simetricul originii O față de punctul A determinați aria triunghiului ABC .

(5p)     5. Arătați că numărul \(N=\left( {{n}^{2}}+n+1 \right)\left( {{n}^{2}}+n+3 \right)+1\) este pătratul unui număr natural par pentru orice număr natural n .

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Un joc de tip ȘOTRON este desenat cu vopsea pe astfalt după schema din figura 2 . Desenul este format din 9 pătrate identice și un cerc ce are diametrul egal cu segmentul AB iar dreptunghiul ABCD are aria de \(50d{{m}^{2}}\).

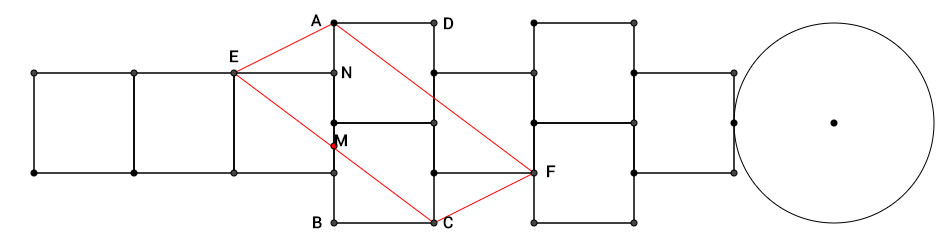
 (5p)  a) Determinați lungimea maximă a desenului pe astfalt .

 (5p)  b) Liniile șotronului sunt evidențiate cu vopsea albă . Știind că pentru fiecare metru trasat se folosește 1,5 cl de vopsea , verificați dacă ajunge o cutie de vopsea cu capacitatea de 250 ml . (\(3,14\le \pi \le 3,15\))

 (5p)  c) Determinați aria patrulaterului AFCE .

2. O bucată de plastilină este modelată după o formă sferică cu diametrul de 12 cm ca în figura 3 .

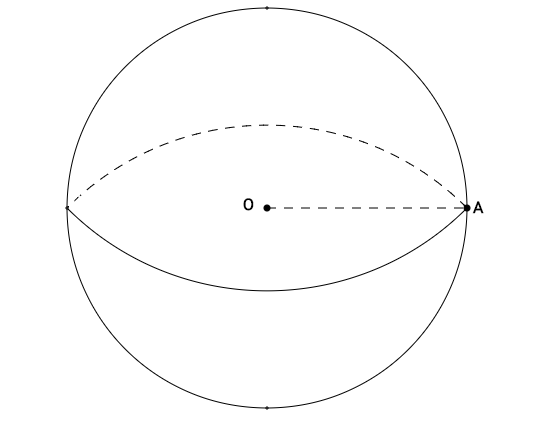
(5p)  a) Aflați aria sferei .

(5p)  b) Câte biluțe sferice cu raza de 5 mm se pot remodela din această bunată de plastilină .

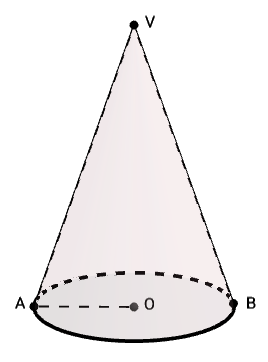
(5p)  c) Remodelând plastilina obținem un con cu aceeași rază ca și sfera inițială . Știind că secțiunea axială a conului este un triunghi dreptunghic isoscel , determinați raportul dintre aria sferei și aria totală a conului obținut .