Varianta 200

Prof: Pisică Lăcrămioara

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \({{\left( 1-0,5 \right)}^{2}}\cdot 4\) este egal cu ... .

(5p)     2. Dacă 8 elevi termină un proiect în 15 ore de atunci avem nevoie de ... elevi pentru a termina proiectul în 12 ore .

(5p)     3. Considerând mulțimile \(A=\left\{ 1;2;3;4;5 \right\}\) și \(B=\left\{ x\in \mathbb{N}|x<3 \right\}\)avem \(A\bigcap B=\left\{ ... \right\}\).

(5p)     4. Suplementul unui unghi cu măsura de \(95{}^\circ 30'\) va avea măsura de ...\({}^\circ \) .

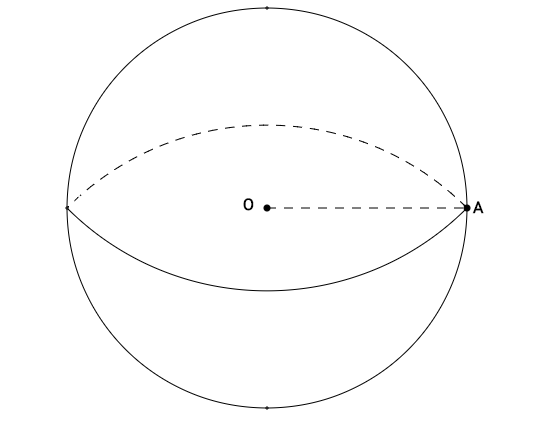
(5p)     5. În figura 1 este reprezentată o sferă cu diametul de 6 cm . Aria sferei va fi egală cu ... cm² .

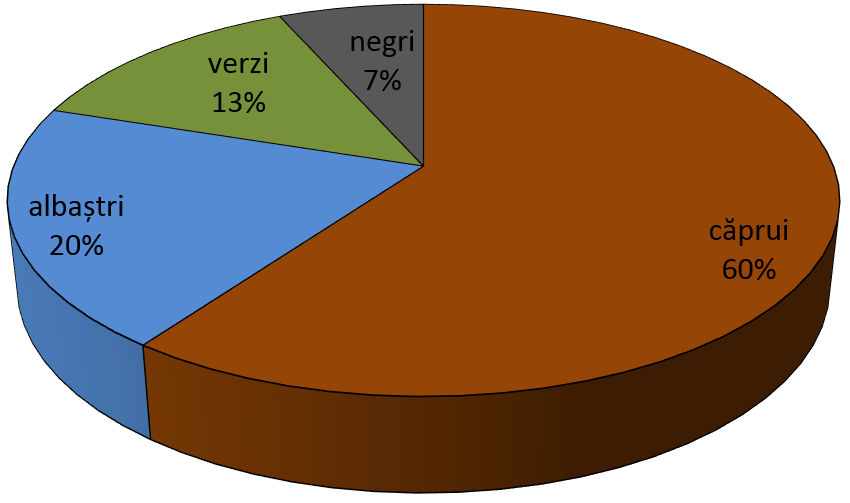
(5p)     6. În diagrama de mai jos este reprezentată repartiția elevilor unei clase după culoarea ochilor.

Dacă în clasă avem 18 de elevi cu ochi căprui atunci numărul elevilor din clasă este de ... .

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenați pe foaia de examen , prisma patrulateră COMPILAT .

(5p)     2. Se dau mulțimile \(A=\left\{ x\in \mathbb{R}|\left| 2x+1 \right|<5 \right\}\) și \(B=\left\{ x\in \mathbb{N}{}^{*}|2-x\ge 0 \right\}\). Determinați cardinalul mulțimii \(A\bigcap B\) .

(5p)     3. Tatăl a doi copii are 38 de ani , iar unul dintre copii este cu 4 ani mai mic decât celălalt . Știind că peste 6 ani tatăl va avea vârsta egală cu dublul sumei vârstelor copiilor săi aflați ce vârstă are fiecare copil în prezent.

 4. Fie expresia \(E(x)=\frac{{{\left( 2x+1 \right)}^{2}}-1}{{{x}^{2}}+2x}:\frac{{{x}^{2}}-1}{x+2}\) , unde \(x\in \mathbb{R}\backslash \left\{ -2;-1;1;0 \right\}\)

(5p)    a) Arătați că \(\left( x-1 \right)\cdot E(x)=4\)

(5p)    b) Determinați numerele naturale n pentru care \(E(n)\in \mathbb{Z}\)

(5p)     5. Fie funcția \(f:\mathbb{R}\to \mathbb{R}\) , \(f(x)=3x-1\). Determinați valoarea parametrului real  m știind că punctul \(A\left( \frac{m+1}{2},m-\frac{1}{2} \right)\) aparține graficului funcției  f .

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

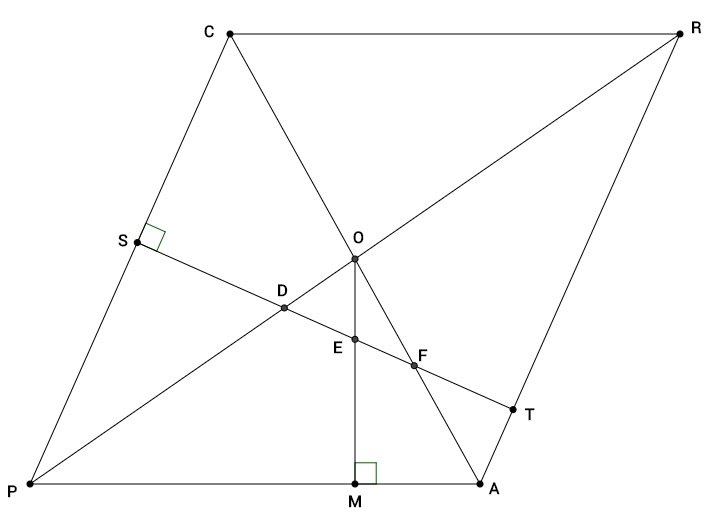
1. În figura 2 este reprezentată schița unui parc sub forma rombului PARC unde AC , PR , ST și OM sunt piste pentru role . Știm că \(\left\{ O \right\}=PR\bigcap AC\) , \(ST\bot PC\) , \(\left( S\in PC,T\in AR \right)\), \(\left\{ D \right\}=ST\bigcap PR\) , \(\left\{ F \right\}=ST\bigcap AC\) , \(OM\bot AP\ (M\in AP)\) , \(\left\{ E \right\}=OM\bigcap ST\) .

 (5p)  a) Știind că \(DL\bot AP\) și \(FN\bot AP\) demonstrați că \(\left[ DS \right]\equiv \left[ DL \right]\)și \(\left[ FT \right]\equiv \left[ FN \right]\) .

 (5p)  b) Demonstrați că \(\left[ OE \right]\equiv \left[ EF \right]\) și \(\left[ OE \right]\equiv \left[ DE \right]\)

 (5p)  c) Un roler pleacă din punctul S și ajunge în T rulând pe pista ST . Un alt roler pleacă din punctul D , ajunge în punctul E , se duce până în punctul M și se întoarce apoi se oprește în punctul F . Dacă cei doi roleri rulează cu aceeași viteză constantă să se determine care termină mai repede traseul .

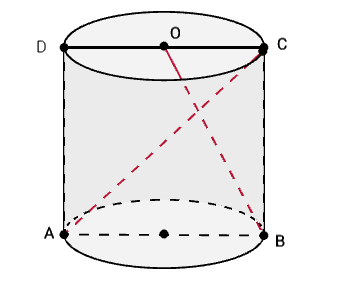
2. În figura 3 este reprezentată o buturugă de forma unui cilindru circular drept cu secțiunea axială pătratul ABCD .Știm că perimetrul pătratului este de 40 dm .

(5p)  a) Arătați că aria bazei cilindrului este egală cu \(25\pi d{{m}^{2}}\) .

(5p)  b) Determinați raportul ariilor triunghiurilor AMB și CMO unde \(\left\{ M \right\}=AC\bigcap BO\) .

(5p)  c) Știind că densitatea lemnului este de \(0,75kg/{{m}^{3}}\) iar \(\pi =3,14\)arătați că buturuga cântărește peste o jumătate de kg