Varianta 150

Prof: Ricu Ileana

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1.Valoarea de adevăr a propozitiei

,, numǎrul$x=\sqrt{{{\left( \sqrt{5}-5 \right)}^{2}}}+\sqrt{30+10\sqrt{5}}+$ $+\sqrt{{{\left( 3-2\sqrt{2} \right)}^{2}}}+\sqrt{18-8\sqrt{2}}\in \mathbb{Z}$ “este………………

(5p)     2. Mulţimea soluţiilor ecuatiei $\sqrt{{{\left( 2x-3 \right)}^{2}}}=25$este………………………………..

(5p)     3 Dacă 25% din x este 4, atunci x=.........................................

(5p)     4. În figura următoare,[AB]este diametrul semicercului k iar C este un punct oarecare pe semicerc situat între A şi B iar S este centrul cercului înscris în triunghiul ABC. Măsura unghiului ASB este de........................

(5p)     5. Se scrie o cifră oarecare în dreapta lui 2010.Care este probabilitatea ca numărul obţinut să fie divizibil cu 3 ?

(5p)     6. Cei 480 elevi ai unei şcoli sunt chestionaţi referitor la numărul de ore petrecut în faţa televizorului într-o săptămână;datele anchetei sunt cuprinse în tabelul de mai jos.Stabiliţi,în procente,câţi elevi urmăresc emisiunile TV peste 12 ore pe săptămână?

 SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Dacă $a\in \left( 2;5 \right),$ calculaţi valoarea expresiei:E=$\sqrt{{{a}^{2}}-4a+4}+\sqrt{{{a}^{2}}-10a+25}$.

(5p)     2.Determinaţi x din figura de mai jos:   

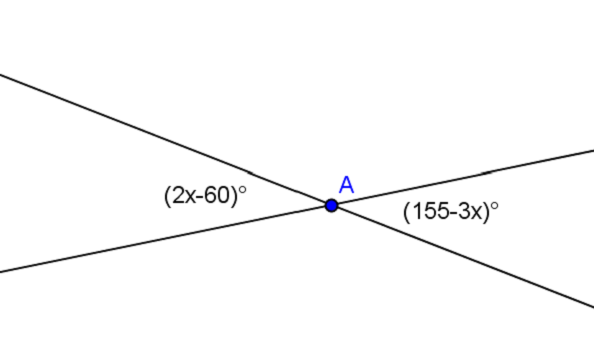
(5p)   3. Într-o clasă sunt 30 elevi, băieţi şi fete. Dacă în clasă vin 3 fete si pleacă 5 băieti,atunci numărul fetelor devine egal cu triplul numărului băieţilor. Să se afle câti băieţi şi câte fete sunt în clasă

4. . Se dă mulţimea $A=\left\{ \text{ }3,\text{ }{{3}^{2}},\text{ }{{3}^{3}},\ldots ,\text{ }{{3}^{2007}} \right\}$. Notăm S suma elementelor mulţimii A.

(5p)    a) Aflaţi suma tuturor resturilor ce se obţin împărţind fiecare element din A la 4.

(5p)    b)  Aflaţi restul împărţirii numărului S la 4.

(5p)     5. Piramida triunghiulară regulată VABC are apotema bazei de $2\sqrt{3}$cm şi muchia laterală formează cu planul bazei un unghi de 60$^{0}$.Calculaţi distanţa de la centrul bazei la o faţa laterală .

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Fie triunghiul ABC dreptunghic în C. Dacă MC este perpendiculară pe planul (ABC) şi

MC = AC = BC = 4 cm, atunci:

(5p)  a) calculaţi distanţa de la M la AB;

(5p)  b) aflaţi aria triunghiului MAB;

(5p)  c) determinaţi distanţa de la C la planul (MAB). 

2. Considerăm un bazin de înot în formă de paralelipiped dreptunghic cu dimensiunile de 50 m , 14 m şi 2 m.

(5p)  a) Calculaţi diagonala bazinului.

(5p)  b) Care este suprafaţa interioară a bazinului ce trebuie faianţată?

(5p)  c) Interiorul bazinului se faianţează cu plăci de faianţă ce au suprafaţa de 40 cm². Care este costul lucrării, ştiind că o cutie conţine 20 de plăci de faianţă şi costul unei cutii este de 15 lei?