Varianta 166

Prof: Iuliana Traşcă

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. A 2010-a zecimală a numărului 2,(75) este.....

(5p)     2. Într-o urnă sunt 15 bile albe, 10 bile roşi, 5 verzi, probabilitatea ca la o extragere să iasă o bilă albă este...

(5p)     3. Suplementul unghiului ${{143}^{0}}{{15}^{'}}24''$este...

(5p)     4. Calculând 15 % din 400 se obţine...

(5p)     5. Aria unui trapez este 345 cm², iar înălţimea are lungimea de 15 cm. Linia mijlocie  a trapezului are lungimea egală cu....cm

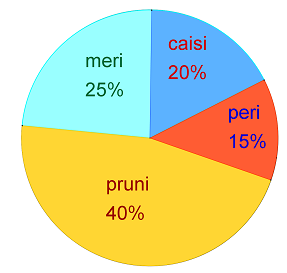
(5p)     6. Într-o livadă sunt pomi fructiferi conform diagramei alăturate. Dacă livada are 4000 pomi fructiferi, atunci numărul merilor este...

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o prismă triunghiulară regulată ABCA^’B^’C^’ şi înălţimea sa OO^’.

(5p)     2. Numerele x, y, z sunt invers proporţionale cu 2, 3, 5. Să se determine aceste numere ştiind  că  x+y+z=62.

(5p)     3. Suma a două numere este 300. Dacă primul număr se măreşte cu10% , iar al doilea se micşorează cu 10% suma lor va deveni 312. Să se afle cele două numere.

4. Fie $f:\mathbb{R}\to \mathbb{R}$, f(x)= 3x+1.

(5p)    a) Arătaţi că $f(a)+f(b)-3\cdot f\left( \frac{a+b}{3} \right)=-1$ oricare ar fi a,b $\in \mathbb{R}$

(5p)    b) Determinaţi n$\in \mathbb{N}$astfel încât f(1)+f(2)+...+f(n)=650.

(5p)     5. Aflaţi valoarea maximă a expresiei E(x)= $\frac{3{{x}^{2}}+18x+34}{{{x}^{2}}+6x+11}$ şi valoarea lui x pentru care se  obţine acest maxim.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

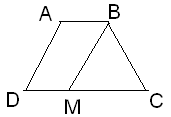
1. Un muncitor are o bucată de tablă de forma unui trapez isoscel ABCD, cu măsura unghiului  obtuz de 120$^{0}$, conform figurii alăturate. El taie tabla după dreapta BM, astfel încât ABMD să fie paralelogram, AD= 8 m şi DM=x m.                           

 (5p)  a) Aflaţi aria tablei  ABCD în funcţie de x;

 (5p)  b) Aflaţi x ştiind că aria tablei ABMD este 50% din aria tablei ABCD;

 (5p)  c) Dacă 1 m² de tablă costă 15 lei , sunt suficienţi 1000 lei pentru a cumpăra toată  tabla ABCD?

2. Un bazin de apă  are formă unui paralelipiped dreptunghic cu dimensiunile L= $\left( \frac{6}{\sqrt{8}}+\frac{4}{2\sqrt{2}} \right)\cdot 4\sqrt{2}$ m,  l = 1,5 dam şi  h= 500 cm

(5p)  a) Câte plăci de gresie de formă pătratică cu latura de 0,05 dam sunt necesare pentru a pava podeaua  bazinului?

(5p)  b) Aflaţi câţi litri de apă sunt în bazin, dacă  apa ocupă 60% din volumul bazinului.

(5p)  c) Dacă diagonala bazinului este $\left( \sqrt{27}-\sqrt{2} \right)\cdot \left( 3\sqrt{3}+\sqrt{2} \right)\cdot \sqrt{2}$, iar dimensiunile bazei rămân aceleaşi, aflaţi înălţimea bazinului..