DREPTE PERPENDICULARE

Definiţie: Două drepte concurente care formează un unghi drept se numesc drepte perpendiculare.

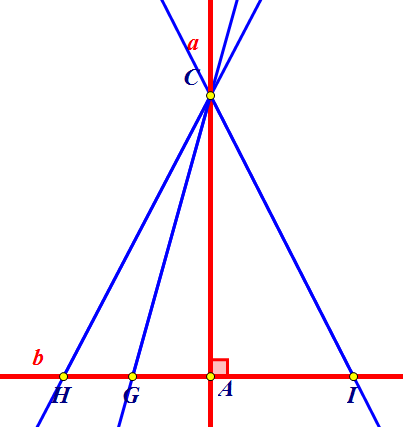
Definiţie:  Spunem că dreapta a este perpendiculară pe dreapta b şi scriem: \(a\bot b\Leftrightarrow m(\sphericalangle a,b)={{90}^{0}}\)

\(Fie\,o\,dreapt\breve{a}\,b\,și\,un\,punct\,C\notin b\)

Dacă prin C construim \(a\bot b\,și\,a\cap b=\{A\}\) , spunem că A este piciorul perpendicularei „coborâte” din punctul C pe dreapta \(b\) .

De reţinut!

Dintr-un punct exterior unei drepte se poate duce (coborî) o perpendiculară şi numai una la acea dreaptă.

Definiţie:  Două drepte care se intersectează şi nu sunt perpendiculare, sunt oblice.

De exemplu dreptele CH, CG, CI sunt drepte  oblice.