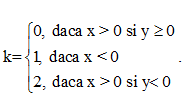Forma trigonometrică a unui numar complex

  Pentru orice numar complex nenul z= x+ iy exista si sunt unice numerele reale r >0 si \(\varphi \)\(\in \)[0,2\(\pi \)) astfel incat z = r(cos\(\varphi \)+isin\(\varphi \)).

Avem r = |z|=\(\sqrt{{{x}^{^{2}}}+{{y}^{2}}}\) si \(\varphi \)= arctg\(\left( \frac{y}{x} \right)+k\pi \), unde 

Daca x = 0 si y >0, atunci \(\varphi \)=\(\frac{\pi }{2}\); daca x = 0 si y < 0, atunci \(\varphi \)=\(\frac{3\pi }{2}\).