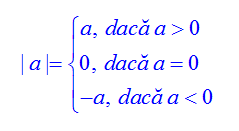MODULUL UNUI NUMĂR REAL. PROPRIETĂȚI.
PROPRIETĂȚI:
1. \(\left| a \right|\ge 0,\mathop{{}}^{{}}\forall a\in R\);
2. \(\left| a \right|=0,\mathop{{}}^{{}}\Leftrightarrow a=0\);
3.\(\left| a \right|=\left| -a \right|,\mathop{{}}^{{}}\forall a\in R\);
4. \(\left| a \right|=\left| b \right|,\mathop{{}}^{{}}\Leftrightarrow a=\pm b\);
5. \(\left| a\cdot b \right|=\left| a \right|\cdot \left| b \right|\);
6. \(\left| \frac{a}{b} \right|=\frac{\left| a \right|}{\left| b \right|}\);
7. \(\left| \left| a \right|-\left| b \right| \right|\le \left| a\pm b \right|\le \left| a \right|+\left| b \right|\);
8. \(\left| x \right|=a,\mathop{{}}^{{}}\Rightarrow x=\pm a,\mathop{{}}^{{}}a\rangle 0\);
9. \(\left| x \right|\le a,\mathop{{}}^{{}}\Leftrightarrow x\in [-a,a],\mathop{{}}^{{}}a\rangle 0\);
10. \(\left| x \right|\ge a,\mathop{{}}^{{}}\Leftrightarrow x\in [-\infty ,-a]\cup [a,+\infty ],\mathop{{}}^{{}}a\rangle 0\).