Varianta 24

Prof: Ionel Brabeceanu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(5\cdot {{5}^{2}}-{{3}^{2}}\cdot {{2}^{2}}\)este ……..

(5p)     2. Suma numerelor naturale impare mai mici decât 12 este ……..

(5p)     3. Probabilitatea ca alegând un element al mulţimii \(\left\{ 0,1,2,3 \right\}\)acesta să verifice inegalitatea \({{n}^{2}}<8\)este …….. 

(5p)     4. Un romb cu diagonalele de \(12cm\) şi \(16cm\) are latura egală cu ……..

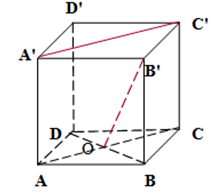
(5p)     5. Se consideră cubul \(ABCD{A}'{B}'{C}'{D}'\)din figura alăturată. Măsura unghiului dintre dreptele \({A}'{C}'\)şi \({B}'O\)este egală cu ……..

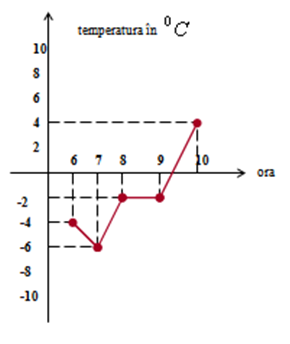
(5p)     6. În figura de mai jos este reprezentată evoluţia temperaturilor între orele 6 şi 10 ale unei zile din luna ianuarie. De la ora 7 până la ora 10 temperatura a crescut cu ……..\(^{0}C\)

    SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Construiţi un paralelipiped dreptunghic \(ABCDEFGH\). 

(5p)     2. Suma a trei numere naturale este \(210\). Se ştie că suma dintre primul şi al doilea număr este de 6 ori mai mare decât al treilea şi că printre cele 3 numere se află şi cel mai mare număr prim de două cifre. Să se afle numerele. 

(5p)     3. Să se rezolve inecuaţia: \(\left( x-2 \right)\left( x+2 \right)-{{\left( x-5 \right)}^{2}}\le 7x+13\). 

           4. Un turist are o sumă \(S\)de bani. Vizitând obiective turistice, în prima zi cheltuieşte \(20%\)din suma \(S\), a doua zi cheltuieşte \(35%\)din suma \(S\), iar a treia zi cheltuieşte \(\frac{1}{4}\)din suma \(S\). 

(5p)    a) Cât la sută cheltuieşte turistul în cele 3 zile? 

(5p)    b) Turistului îi rămân 100 de lei după cele 3 zile. Determinaţi valoarea sumei \(S\); 

(5p)     5. Să se arate că expresia \(E\left( x \right)=2\left( 4x+1 \right)\left( 1-4x \right)+{{\left( 4x-3 \right)}^{2}}+{{\left( 3+4x \right)}^{2}}\)nu depinde de \(x\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

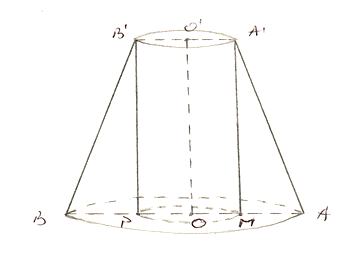
  1. În figura de mai jos este reprezentată o piesă metalică in formă de trunchi de con circular drept cu raza mare de \(12cm\) şi raza mică de \(6cm\) din care se obţine prin prelucrare un cilindru circular drept cu raza bazelor de \(6cm\) şi înălţimea egală cu înălţimea trunchiului.

(5p)  a) Aflaţi aria laterală a trunchiului de con

(5p)  b) Determinaţi volumul cilindrului

(5p)  c) Arătaţi ca lungimea segmentului \(\left[ B{{A}^{'}} \right]\) este mai mică de \(21cm\).

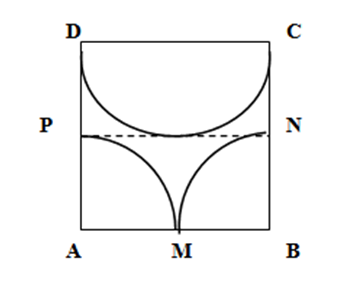
 2. Pentru confecţionarea unui grilaj metalic de formă dreptunghiulară cu lungimea de \(2m\) sunt necesare 60 de bucăţi de forma celui din figură. Se ştie că \(ABCD\)este pătrat cu latura de \(20cm\), iar \(M,N\) şi \(P\)sunt mijloacele laturilor pătratului. 

(5p)  a) Aflaţi lăţimea grilajului; 

(5p)  b) Calculaţi suma lungimilor tuturor arcelor din grilaj exprimată în \(m\); 

(5p)  c) Care este numărul minim de bare metalice de\(2m\)necesare confecţionării tuturor arcelor \(\left( 3,14<\pi <3,15 \right)\);