Varianta 26

Prof: Ionel Brabeceanu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(5,5+0,5:5-1,2\)este ……..

(5p)     2. Numărul natural de forma \(\overline{4x3x}\)divizibil cu 5, \(x\ne 0\), este ……..

(5p)     3. Soluţia în \(\mathbb{N}\)a ecuaţiei \(2-3x=-10\), este \(x=\)…….. 

(5p)     4. În pătratul \(ABCD\)cu latura de \(6cm\), se notează cu \(M\)mijlocul laturii \(AB\)şi cu \(N\)mijlocul laturii \(BC\). Lungimea segmentului \(\left[ MN \right]\)este ……..\(cm\).

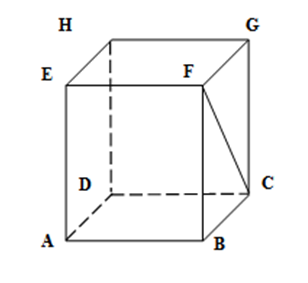
(5p)     5. În figura alăturată, \(ABCDEFGH\)este o prismă dreaptă cu baza pătratul \(ABCD\)de latură \(8cm\)şi \(FC=10cm\). Lungimea segmentului \(\left[ AE \right]\)este egală cu ……..\(cm\). 

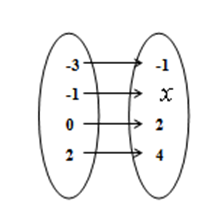
 (5p)     6. În figura de mai jos fiecărui element al mulţimii \(A\)îi corespunde un singur element în mulţimea \(B\). Lui \(-1\)îi corespunde numărul ……..

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o prismă triunghiulară regulată \(ABC{A}'{B}'{C}'\). 

(5p)     2. În trei saci sunt 460 de mere. Numărul merelor din primul sac reprezintă \(\frac{3}{4}\)din numărul merelor din al doilea sac, iar în al treilea sac sunt de \(\frac{3}{2}\)ori mai multe mere decât în primul sac. Câte mere sunt în fiecare sac. 

(5p)     3. \(12%\)din preţul unei mărfi, adică, \(25,4\)lei reprezintă cheltuieli de transport. Care este preţul mărfii? 

           4. Fie funcţia \(f:\mathbb{R}\to \mathbb{R},\text{  }f\left( x \right)=\left( m+2 \right)x+m+1,\text{  }m\in \mathbb{R}\). 

(5p)    a) Să se determine funcţia \(f\) al cărui grafic conţine punctul \(M\left( 0,3m \right)\); 

(5p)    b) Pentru \(m=\frac{1}{2}\)să se calculeze media aritmetică a valorilor \(f\left( 1 \right)\)şi \(\left| f\left( -1 \right) \right|\); 

(5p)     5. Să se rezolve ecuaţia: \(\left| x+1 \right|+\left| 2x+2 \right|=3\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

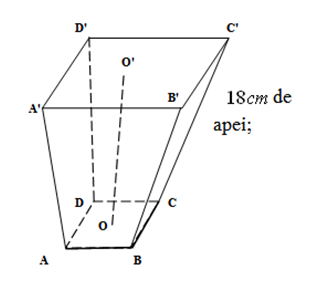
  1. În figura alăturată este reprezentat un vas în formă de trunchi de piramidă patrulateră regulată cu laturile bazelor de \(40cm\), respectiv \(20cm\) şi înălţimea de \(24cm\). 

 (5p)  a) Aflaţi volumul vasului; 

 (5p)  b) Calculaţi aria laterală a trunchiului de piramidă; 

 (5p)  c) Se toarnă în vas \(13,95l\)apă care se va ridica la \(18cm\)de baza mică. Determinaţi aria pătratului ce reprezintă suprafaţa apei;

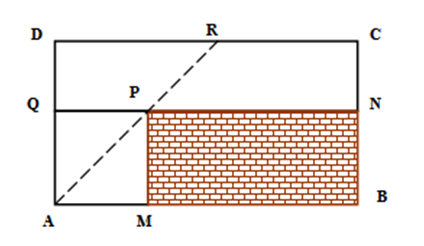
    2. Dreptunghiul \(ABCD\) reprezintă o curte în care porţiunea haşurată este un dreptunghi rezervat pentru construcţia casei, iar pătratul \(AMPQ\) este semănat cu gazon. Se ştie că \(AB=40m\), \(BC=25m\), \(AM=15m\), iar \(AP\cap CD=\left\{ R \right\}\). 

(5p)  a) Calculaţi cât la sută reprezintă suprafaţa pătratului din suprafaţa totală a curţii; 

(5p)  b) Aflaţi aria patrulaterului \(ABCR\); 

(5p)  c) Determinaţi distanţa \(PR\);