Întrebare TRAPEZ

Buna ziua
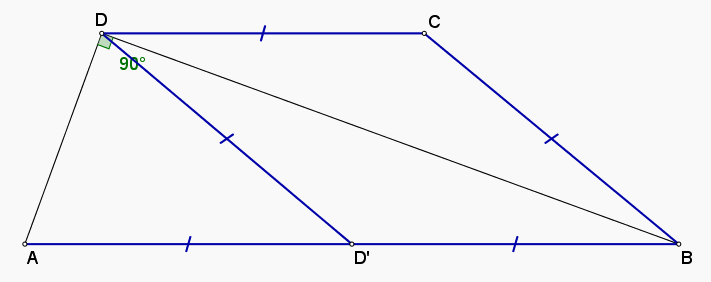
In trapezul ABCD ,AB || CD,AB>CD,CD=BC=6 cm,iar BD este perpendicular pe AD.
a)Aratati ca AB=2CD
b)Daca E si F sunt proiectiile punctelor D respectiv C pe AB si
FB=2AE calculati AD si BD.
multumesc

Buna ziua,

a). Vedeti primul desen.

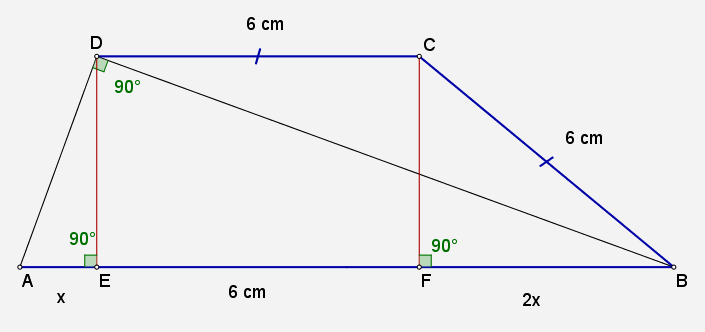
b). Pe al doilea desen: in triunghiul $CFB$, $CF^{2}=36-4x^{2}$.

In triunghiul $ADB$ scriem Teorema inaltimii: $DE^{2}=AE \cdot EB$. Cum $DE=CF$, putem scrie ca $36-4x^{2} = x\cdot \left (6+2x \right )$. Rezolvati ecuatia (considerati corecta solutia pozitiva), si obtineti $x$=....? Mai departe e simplu.

Deci: AD = ...? BD = ....?

Buna seara
Am inteles.
Daca nu am gresit a rezultat:
x=2 cm;
$$AD=\sqrt{4+20}=2\sqrt{6}cm$$

BD=6 cm
AD se rezolva prin teorema lui Pitagora.
Multumesc

Buna seara
Totusi ma framanta o intrebare si m-am gandit sa va supar si sa o pun.
Nu am inteles de ce FB=2x?
multumesc

Pentru ca FB=2AE si am notat AE=x.

Completare: BD n-are cum sa fie 6. Mai verificati o data socotelile.

$$Din\ \triangle BDE\rightarrow BD=\sqrt{BE^2+ED^2}=\sqrt{100+20}\\ BD=2\sqrt{30}\ cm.$$
Am observat si eu eroarea dar deja transmisesem raspunsul.
Cred ca acum este bine.
Insa imi cer mii de scuze tot nu am inteles de ce FB=2x in ipoteza ca notam AE=x?
sau mai bine zis de ce FB=2AE?
multumesc mult pentru bunavointa.