Întrebare Distanta dintre 2 plane

Buna ziua,

Am o problema scurta si ciudata.

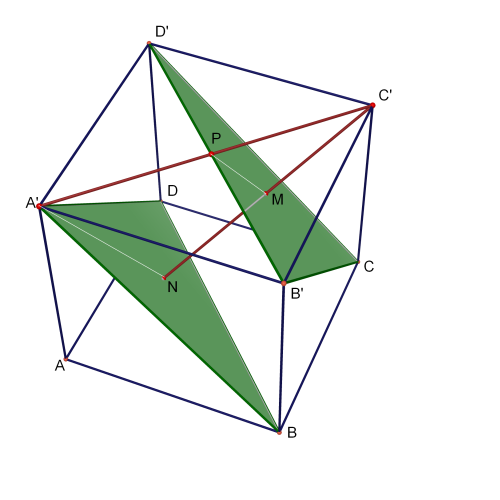
Fie cubul ABCDA'B'C'D' de muchie 12 cm. Calculati d((A'BD);(B'D'C)).

Banuiesc ca e o treime din diagonala cubului, dar nu vad cum sa demonstrez ca ea e perpendiculara si nici cum sa calculez aceasta distanta.

Daca aveti sugestii, va multumesc mult!

Confirm bănuiala ta, dar nu e uşor de demonstrat. Observăm că planul (A'BD) este paralel cu planul (B'D'C), ceea ce rezultă din teorema beţelor chinezeşti ( matefix.ro/lectie-698 ). De aici rezultă că înălţimea tetraedrului B'D'CC' este perpendiculară pe (A'BD) deci d((A'BD);(B'D'C))=MN=C'M; ultima egalitate rezultă din faptul că PM este linie mijlocie în triunghiul A'C'N. Pentru a calcula C'M scriem volumul tetraedrului B'D'CC' în două moduri: \(V_{B'D'CC'}=\frac{C'M\cdot A_{B'D'C}}{3}=\frac{C'D'\cdot A_{B'CC'}}{3}\) de unde obţinem \(MN=C'M=\frac{l\sqrt{3}}{3}=\frac{BD'}{3}=4\sqrt{3}\) cm.