Întrebare Problema geometrie

Fie triunghiul ABC cu unghiul A = 90 . Se considera AD perpendicular pe BC. Aratati ca masura lui BCA este de 15 daca si numai daca : 4 AD la puterea 2 = AC . AB

Va multumesc anticipat de ajutor!

Buna ziua,

Folosind Teorema catetelor si Teorema inaltimii, se poate scrie

$4AD^{2}=AC\cdot AB\Leftrightarrow 4AD^{2}=\sqrt{DC\cdot BC}\cdot \sqrt{BD\cdot BC}\Leftrightarrow$

$4AD^{2}=BC\cdot AD\Leftrightarrow AD=\frac{BC}{4}$.

Prima data demonstram implicatia $m\left (\angle BCA \right )=15^{o}\Rightarrow AD=\frac{BC}{4}$.

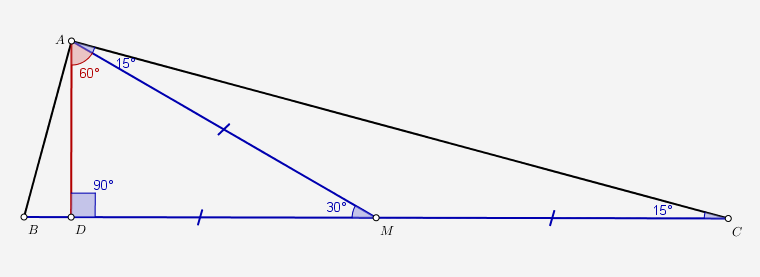
Aveti atasat un desen: M este mijlocul laturii [BC]. Atunci triunghiul AMC este isoscel (AM=MC) => $m\left (\angle MAC \right )=m\left (\angle MCA \right )=15^{o}$.
Mai departe $m\left (\angle AMD \right )=30^{o}$ ($=180^{o}-150^{o}$).

In triunghiul dreptunghic ADM, folosim Teorema unghiului de 30:

.

Cealalta implicatie, $AD=\frac{BC}{4}\Rightarrow m\left ( \angle CBA \right )=15^{o}$, se demonstreaza similar:

Se ia mijlocul lui [BC], atunci $AD=\frac{BC}{4}=\frac{AM}{2}$, deci $m\left ( \angle AMD \right )=30^{o}$ $\Rightarrow m\left ( \angle AMC \right )=180^{o}-30^{o}=150^{o}$.

Dar, cum triunghiul AMC este isoscel ($AM=MC=\frac{BC}{2}$), avem ca $m\left ( \angle ACM \right )=\frac{180^{o}-150^{o}}{2}=15^{o}$.

Va multumesc muuuuult!
Un an 2016 cat mai bun sa aveti!