Întrebare Plane perpendiculare

Triunghiul ABC isoscel,AB=AC=25 cm si BC=30 cm ,se indoaie dupa inaltimea [BE] pana cand planul (ABE) este perpendicular pe planul (BEC). Calculati tangenta unghiului plan corespunzator diedrului format de planele (ABC) si (BEC) dupa indoire.

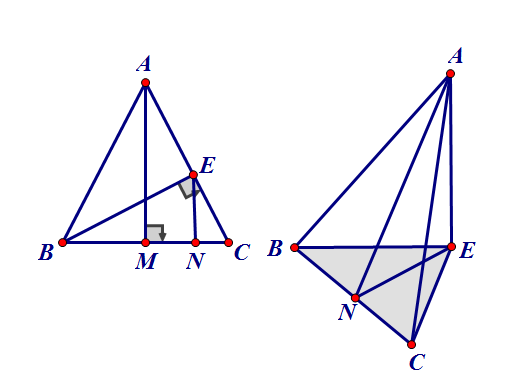
În figura plană
Fie \(AM\bot BC\)
\(\Delta ABC\,isoscel\,\Rightarrow \) [AM] mediană și înălțime,deci BM=MC=15cm
\(\Delta AMB\,,\,m(\sphericalangle M)={{90}^{0}}\Rightarrow \,(T.P.)\,AM=20cm\)
\(BC\cdot AM=AC\cdot BE\Rightarrow BE=24cm\)
\(\Delta AEB,m(\sphericalangle E)={{90}^{0}}\Rightarrow (T.P.)AE=7cm\)

Îndoim triunghiului după înălțime și obținem figura în spațiu
\((AEB)\cap (BEC)=BE,\,(AEB)\bot (BEC),AE\bot BE\Rightarrow \)
\(AE\bot (BEC)\)
Fie \(EN\bot BC,EN,BC\subset (BEC)\overset{{{T}_{3}}P}{\mathop{\Rightarrow }}\,AN\bot BC\)
\((ABC)\cap (BEC)=BC,\,AN\bot BC,EN\bot BC\Rightarrow \)
Unghiul căutat este \(\sphericalangle ANE\)
\(EN=\frac{BE\cdot EC}{BC}=\frac{72}{5}\) (în plan)
\(tg(\sphericalangle ANE)=\frac{AE}{NE}=\frac{35}{72}\) (în spațiu)