Întrebare geometrie

Fie ABC un triunghi dreptunghic in A si avand laturile, respectiv, a,b,c. Triunghiul se roteste in jurul ipotenuzei [BC] obtinandu-se un corp K. In acest corp se inscrie o sfera S1 si se circumscrie o sfera S2. Determinati:
i)Razele r1 si r2 ale celor doua sfere.
ii)Distanta dintre centrele celor doua sfere

Buna ziua,

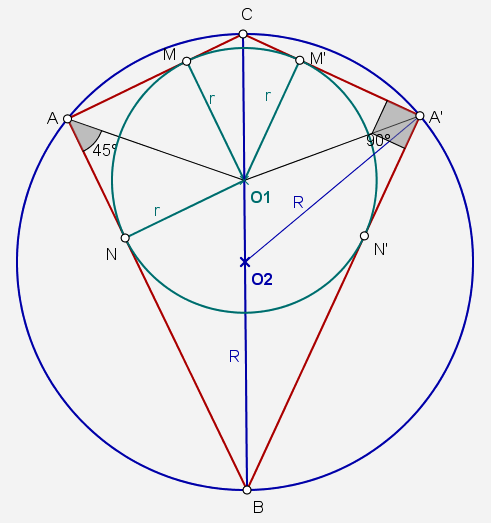
Aveti atasat un desen:
In triunghiul \(ABC\), \(m\left ( \widehat{A} \right )=90^{o}\), \(a>c>b\), \(O_{1}\) este centrul sferei \(S_{1}\), si \(O_{2}\) este centrul sferei \(S_{2}\).

\(i\)). Raza sferei circumscrise (\(S_{2}\) ) este jumatatea ipotenuzei, adica \(\frac{a}{2}\) (fiind vorba de un triunghi dreptunghic, poate fi inscris intr-un semicerc), deci \(R=\frac{a}{2}\).

Centrul sferei inscrise in corp se situeaza pe ipotenuza. Raza acestei sfere este latura patratului inscris in triunghiul \(ABC\). Fiind vorba de un patrat, \(AO_{1}\) este bisectoarea unghiului \(BAC\). Exista formula pentru a afla lungimea bisectoarei unui triunghi:

\(AO_{1}=l_{a}=\frac{2}{b+c}\sqrt{bcp\left ( p-a \right )}\), \(p=\frac{a+b+c}{2}\).

Fiind vorba de un triunghi dreptunghic, avem

\(p\left ( p-a \right )=\frac{\left ( b+c+a \right )\left ( b+c-a \right )}{4}=\frac{b^{2}+c^{2}-a^{2}+2bc}{4}=\frac{2bc}{4}\), deci \(AO_{1}=\frac{2}{b+c}\sqrt{\frac{2\left (bc \right )^{2}}{4}}=\frac{bc}{b+c}\sqrt{2}\).

\(AO_{1}\) este ipotenuza in patratul \(ANO_{1}M\), deci \(AO_{1}=O_{1}M\sqrt{2}\Rightarrow O_{1}M=\frac{bc}{b+c}\), adica \(r=\frac{bc}{b+c}\).

Avem, deci: \(r=\frac{bc}{b+c}\) si \(R=\frac{a}{2}\).

\(ii\)). Pentru a afla distanta dintre cele doua centre (adica \(O_{1}O_{2}\)), calculam \(O_{1}C\) cu ajutorul Teoremei bisectoarei (in triunghiul \(ABC\), in cazul bisectoarei \(AO_{1}\). Notam \(O_{1}C=x\).

\(\frac{AC}{AB}=\frac{O_{1}C}{O_{1}B}\) \(\Leftrightarrow \frac{b}{c}=\frac{x}{a-x}\), de unde \(x=\frac{ab}{b+c}\). Atunci \(O_{1}O_{2}=CO_{2}-CO_{1}=\frac{a}{2}-\frac{ab}{b+c}=\frac{a}{2}\cdot \frac{c-b}{b+c}\).

Distanta dintre centre: \(O_{1}O_{2}=\frac{a}{2}\cdot \frac{c-b}{b+c}\).

Observatie: acum vad ca in enunt razele sferelor sunt notate cu \(r_{1}\) respectiv \(r_{2}\), in loc de \(r\) si \(R\) .

Multumesc!