×
Indicații, rezolvări și soluții pentru problemele și exercițiile de liceu.
 Întrebare
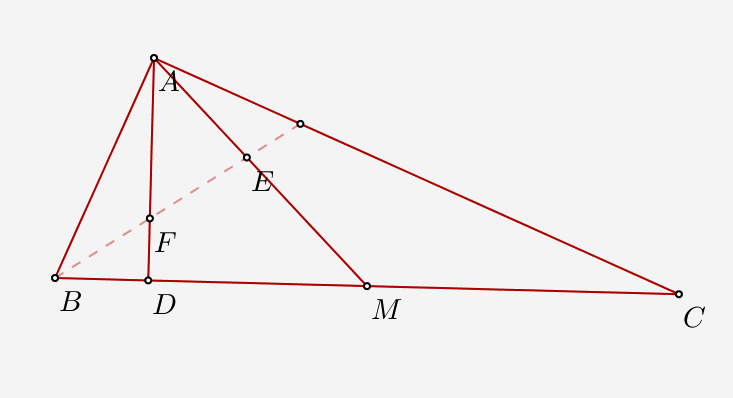
Geometrie cl.a 9-a Teorema bisectoarei
Întrebare
Geometrie cl.a 9-a Teorema bisectoarei
Acces Forum
- Nepermis: pentru a crea subiect nou.
- Nepermis: pentru a răspunde.
- Nepermis: pentru a adăuga atașamente.
- Nepermis: să-ți editeze mesajele.
Timp creare pagină: 0.100 secunde